Question

A ball is dropped from height ‘h’. If the coefficient of restitution be ‘e’, then to what extent will the height rise after jumping twice from the ground?
A. $\dfrac{{{\text{eh}}}}{2}$
B. $2eh$
C. $eh$
D. ${{\text{e}}^4}.{\text{h}}$

Answer 1

Hint: Find the velocity of ball just before first collision by third equation of motion and just after collision by formula of coefficient of restitution ($e = \dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}}$) by using ground velocity to be zero before and after the collision. Again find the velocity of the ball after the 2nd collision using the formula of restitution (just before the 2nd velocity is the same as it was after just after 1st collision). Finally find the height to which the ball rises by the third equation of motion.

Step by step answer:

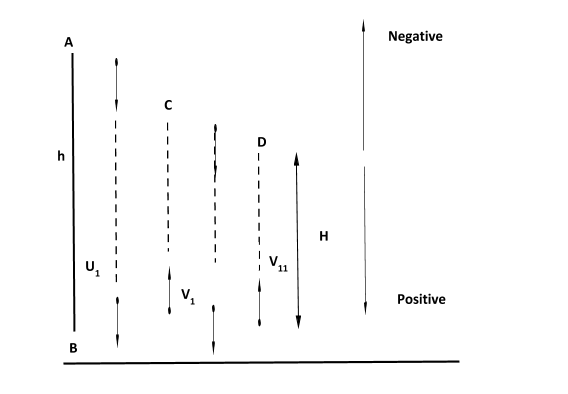
Let's say the ball is dropped from A, so it’s velocity is zero. It strikes the ground and reaches upto point C. It again goes down and after striking the ground it reaches point D. So we have to find the height of point D from ground. Also let us consider upward direction as negative and downward direction as positive.( We are free to choose any direction to be positive or negative).
So, first let us find the velocity of the ball just before striking the ground for the first time. Let us call it ‘${{\text{u}}_1}$’. Also let us assume downward direction as positive and upward as negative.
Let’s analyse the motion from A to B.
u = 0
a = g
S = h
v = ${{\text{u}}_1}$
where, a is acceleration, s is displacement and v is final velocity
So, from the third equation of motion we get,
${{\text{v}}^2} - {{\text{u}}^2} = 2{\text{as}}$
${\text{u}}_1^2 - 0 = 2\left( {\text{g}} \right)\left( {\text{h}} \right)$
$\Rightarrow {{\text{u}}_1} = \sqrt {2{\text{gh}}}$……….. equation (1)
So, after striking the ground, let's say its velocity becomes${{\text{v}}_1}$.
Now coefficient of restitution is given by:
$e = \dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}}$
where, ${\text{ }}{{\text{v}}_1}$and ${{\text{v}}_2}$are final velocities, ${{\text{u}}_1}$and ${{\text{u}}_2}$are initial velocities of two bodies after and before collision respectively. Here, second body is ground which always remain at rest, therefore ${{\text{u}}_2}$= ${{\text{v}}_2}$= 0
Therefore,
${\text{e = }}\dfrac{{ - {{\text{v}}_1}}}{{{{\text{u}}_1}}}$
${\text{e = }}\dfrac{{ - {{\text{v}}_1}}}{{\sqrt {2{\text{gh}}} }}$ (From equation 1)
${{\text{v}}_1} = - {\text{e}}\sqrt {2{\text{gh}}}$ ……….. equation (2)

Here negative sign is indicating that velocity is upwards
Now the speed with which a body comes back to ground is the same as the speed with which it goes up if it is under the influence of gravity alone, therefore the ball will return to ground with speed ${v_1}$.
Now again using the formula for coefficient of restitution:
$e = \dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}}$
$e = \dfrac{{0 - {v_{11}}}}{{{v_1} - 0}}$
here ${v_{11}}$ is velocity of ball after collision. Be careful that we will use ${v_1}$to be positive here because its direction is downwards before the 2nd collision. So put positive value of ${v_1}$ from 2nd equation
$e = \dfrac{{ - {v_{11}}}}{{e\sqrt {2gh} }}$
${v_{11}} = - {e^2}\sqrt {2gh}$
Now the ball reaches point D. So the final velocity of the ball is zero.
Therefore from ground to point D
u = ${v_{11}} = - {e^2}\sqrt {2gh}$
v = 0
a = g
Now, from third equation of motion
${{\text{v}}^2} - {{\text{u}}^2} = 2{\text{as}}$
$0 - {\left( {{{\text{e}}^{^2}}\sqrt {2{\text{gh}}} } \right)^2} = 2\left( {\text{g}} \right)\left( {\text{s}} \right)$
${\text{s = }}\dfrac{{ - {{\text{e}}^4}\left( {2{\text{gh}}} \right)}}{{2{\text{g}}}}$ = $- {{\text{e}}^4}{\text{h}}$
Negative sign indicating upward direction.
Hence, H = ${{\text{e}}^4}{\text{h}}$
So, the option ‘d’ is the correct answer.

Note: This equation can be solved only by a direct formula. Height of ball after nth collision with ground is given by H = ${\text{h}}{{\text{e}}^{2{\text{n}}}}$ where, h is original height from it is dropped and n is the number of collisions with ground.
Here, n = 2
Therefore, H = ${\text{h}}{{\text{e}}^{2\left( 2 \right)}}$
H = ${\text{h}}{{\text{e}}^4}$