Question

A ball is dropped from a high rise platform at $t=0s$ starting from rest. After 6 seconds another ball is thrown downwards from the same platform with a speed v. The two balls meet at $t=18s$ . What is the value of v? (Take $\text{g=10 m / }{{\text{s}}^{\text{-2}}}$ )

Answer 1

To solve this question, we should use the formula relating to distance and time. We should know that the first body is freely falling and it is having an acceleration downwards due to gravity. In the case of the second body, it is having an initial velocity and the same acceleration due to gravity. We should find the distances travelled by the bodies from the equation of the first body and substitute it for the second one.
Formula used:
$s=ut+\dfrac{1}{2}a{{t}^{2}}$

Complete answer:
Firstly, we will draw a diagram to understand the situation better.

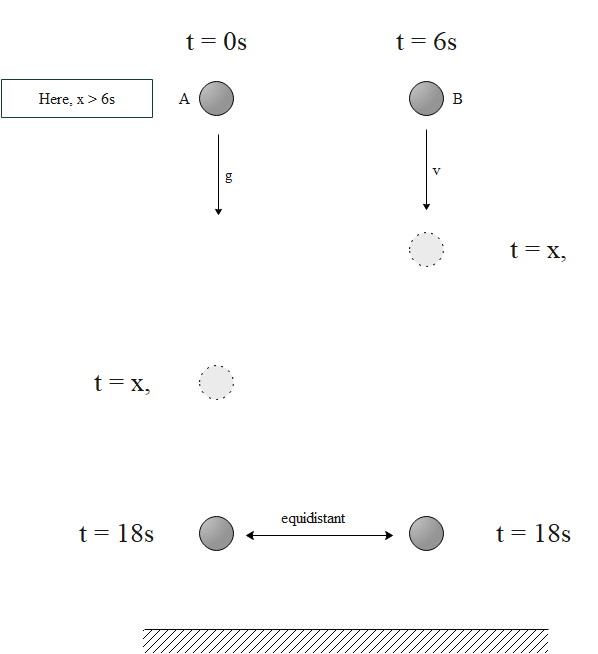
Let us consider that the first situation involves the ball, which is A and the second situation involves the ball which is B.
Let us analyze the first situation, before moving on to the second one.
It is given in the question that,
The vertical distance travelled by the ball A in a time t is 18 seconds (as mentioned in the question).
Now we have to apply the distance and time formula. The distance and time formula is given by,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
In the above mentioned question, the variables denote the following values:
s represents the final distance covered
u represents the initial distance covered
g represents the acceleration due to gravity
and t represents the time taken.
So, putting the values in the equation we get the following expression,
${{s}_{1}}=0+\dfrac{1}{2}\times 10\times {{18}^{2}}=1620m$
(In this expression the variable $s$ represents the distance which is travelled by ball A)
So the distance travelled by the first ball is 1620m.
Now we have to calculate the distance which is travelled by ball B.
In the case of the second ball, we need to consider the fact that ball B travelled in 12 seconds. We can say the time to be 12 seconds because the time is considered from 6 seconds to 18 seconds.
So, now applying the same formula of distance and time we get that,
${{s}_{2}}=12v+\dfrac{1}{2}\times 10\times {{12}^{2}}$
In the above expression, v is the initial velocity of the ball B and ${{s}_{2}}$ is the distance which is travelled by the ball B.
Now, it is given that the distance covered by ball A and ball B is the same at $t=18s$. So, we can write ${{s}_{1}}={{s}_{2}}$.
So now, equating both the distance equation we get that,
${{s}_{1}}={{s}_{2}}$

& \Rightarrow 1620=12v+\dfrac{1}{2}\times 10\times {{12}^{2}} \\\ & \Rightarrow v=\dfrac{1620-\left( \dfrac{1}{2}\times 10\times {{12}^{2}} \right)}{12} \\\ & \Rightarrow v=\dfrac{900}{12}=75m/s \\\ \end{aligned}$$ **Note:** Keep in mind that in the solution, we have assumed that the two balls meet at a height of 1620m from the platform before one of the bodies hits the ground. In this particular case, we have taken all the values as positive by sign convention because the velocity, acceleration, and distance are in the same direction. Which is the same as the direction of motion of the body. So don’t get confused.