Question

A ball is dropped from a height rise platform t=0 starting from rest. After 6s another ball is thrown downwards from the same platform with a speed v. The two balls meet at t=18s. What is the value of v?
A) 75m/s
B) 64m/s
C) 84m/s
D) 94m/s

Answer 1

Use the equation of motion to calculate distance travel by first ball. The time at which two balls meet is the difference in time. Again, use the equation of motion for the second ball to calculate the velocity of the second ball.

Formula used:
Second equation of motion: $s = ut + \dfrac{1}{2}a{t^2}$

Complete step by step answer:
Figure 1 depicts the situation mentioned above.

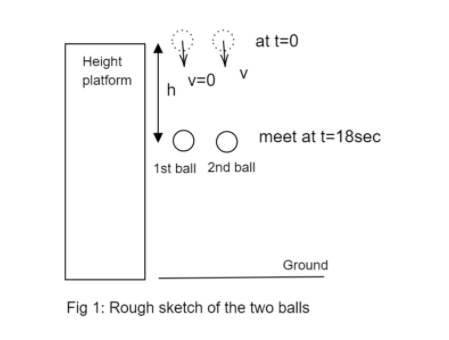
Step1: Using the equation of motion for the first ball to calculate the height travel by it in the first $18s$.
$h = ut + \dfrac{1}{2}g{t^2}$
Given that t=18s, u=0m/s and g=$10m/{s^2}$
Therefore,
$\Rightarrow h = 0 + \dfrac{1}{2} \times 10 \times {\left( {18} \right)^2}$
$\Rightarrow h = \dfrac{1}{2} \times 10 \times {\left( {18} \right)^2} = 1620m$
Step2: Since the second ball is thrown after $6s$ therefore the time after which they meet is $18-6=12s$.
Now to cover same height of $1620m$ in $12$ seconds by second ball, use the equation of motion again
$h = vt + \dfrac{1}{2}g{t^2}$
Where v is velocity with which the second ball is thrown,
Substituting all values in above equation,
$\Rightarrow 1620 = v(12) + \dfrac{1}{2} \times 10 \times {\left( {12} \right)^2}$
Step3: Now simplifying the above equation to calculate the velocity of second ball
$\Rightarrow 1620 = 12v + 720 \\\ \Rightarrow 12v = 900$
On simplification,
$\Rightarrow v = \dfrac{{900}}{{12}} \\\ \Rightarrow v = 75m/s \\\$

Therefore option (A) is the correct answer.

Note:
- In such problems where g is involved, we should take reference for measuring the distance to be ground or another place we wish. But we should focus on two things, the first thing, a relative position from the reference, and the second thing is sign convention with respect to reference should be uniform throughout the problem.
- Always remember that the time after which the two balls meet is the difference in the two times which they individually take to travel.