Question

A ball is dropped from a height of 90m on a floor. At each collision with the floor, the ball loses one-tenth of its speed. Plot the speed-time graph of its motion t= 0 to t = 12s.

Answer 1

We could use Newton’s equations of motion to find the final velocity before the first collision with the floor. Reducing one-tenth of this value from it gives you the rebound velocity. Again you could find the time taken to reach the maximum height after re-bounce. Keeping in mind that the time of ascending will be equal to the time of descent, find the total time taken for the whole process, and repeat it till the total time taken is 12s.
Formula used:
Newton’s equations of motion,
${{v}^{2}}-{{u}^{2}}=2as$
$v=u+at$

Complete step-by-step solution
We see that the ball is dropped from a height s = 90m, so, initial velocity will be,
$u=0$
Also, $g=10m{{s}^{-1}}$
If ${{v}_{1}}$ is the final velocity at first collision, then by Newton’s equations of motion we have,
${{v}^{2}}-{{u}^{2}}=2as$ ……………………………… (1)
$\Rightarrow {{v}_{1}}^{2}-0=2\times 10\times 90$
$\therefore {{v}_{1}}=42.43m{{s}^{-1}}$ ………………………….. (2)
Time taken for the first collision can be given by,
$v=u+at$ ……………………………………. (3)
$\Rightarrow t=\dfrac{42.43}{10}$
$\therefore t=4.24s$ ……………………………………….. (4)
We are said that the ball lose its one-tenth of velocity on each collision, velocity after each collision, that is, the rebound velocity is given by,
${{v}_{r}}=v-\dfrac{1}{10}v$
$\Rightarrow {{v}_{r}}=\dfrac{9}{10}v$ …………………………… (5)
The velocity after first collision will be,
${{v}_{2}}=\dfrac{9}{10}{{v}_{1}}$
$\Rightarrow {{v}_{2}}=\dfrac{9}{10}\left( 42.43 \right)$
$\therefore {{v}_{2}}=38.19m{{s}^{-1}}$
From (3), time taken to reach maximum height (v = 0) after first collision will be,
$0=38.19-10{{t}_{2}}$
${{t}_{2}}=3.81s$
Total time taken by now will be,
$T=8.05s$
Time of ascending will be the same as the time of descending, so, by the second collision the total time taken will be,
$T'=4.24+3.81+3.81=11.86$
Velocity after the second collision will be,
${{v}_{3}}=\dfrac{9}{10}\left( 38.19 \right)$
$\Rightarrow {{v}_{3}}=34.37m{{s}^{-1}}$
Using the above information we could plot the speed-time graph as,

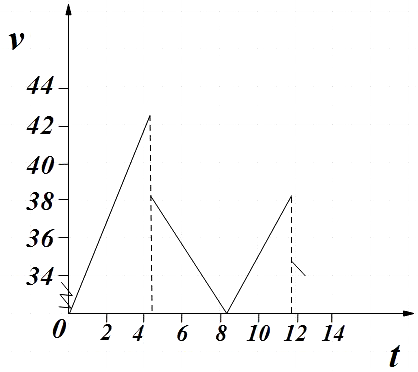
Note: Since we are asked to plot the speed-time graph, both being scalar quantities we shouldn’t worry about the direction while plotting the graph. However, while substituting in the equations of motion we have to take care of the direction of both velocity and acceleration. By convention, the direction of acceleration due to gravity is taken positive downward.