Question

A ball is dropped from a height of 49 m, the wind blows horizontally that accelerates the ball with a constant acceleration of $4.9m{{s}^{-2}}$. Choose the correct statement(s). (consider $g=10m{{s}^{-2}}$)
(this question has multiple correct options)
A. Path of the ball is a straight line
B. Path of the ball is a curved one.
C. The time taken by the ball to reach the ground is 3.16s
D. The angle made by the line joining initial and final position (on the ground 1st strike) of the ball with the horizontal is greater than ${{45}^{\circ }}$.

Answer 1

Since the ball was at rest initially, it will move in a path that is along (parallel to) the direction of the acceleration. To find the time taken for the ball to reach the ground use one of the kinematic equations to the vertical motion of the ball.

Formula used:
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
Here $s$ is the displacement of the ball at time $t$, $u$ is its initial velocity and $a$ is its acceleration.

Complete step by step solution:
When a ball is dropped from a certain height, the ball accelerates downwards under the force of gravity. The magnitude of the acceleration due to gravity is g. However, it is given that wind blows in the horizontal direction. The will exert a force on the ball and accelerate it in the direction of its flow. This acceleration is given to be $4.9m{{s}^{-2}}$.

As a result, the ball will have an acceleration in the downward direction as well in the horizontal direction. The net acceleration of the ball will be the vector of sum of these two accelerations.

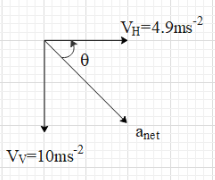
Since the ball was at rest initially, it will move in a path that is along (parallel to) the direction of the acceleration. We know that the acceleration of the ball is constant. This means that the direction of the motion of the ball is fixed. Therefore, the ball will move along a straight line. Hence, option A is correct.

To find the time taken for the ball to reach the ground, we shall use the kinematic equation $s=ut+\dfrac{1}{2}a{{t}^{2}}$ ….. (i) for the downward motion of the ball.
Here $s$ is the displacement of the ball at time $t$, $u$ is its initial velocity and $a$ is its acceleration.
In this case, $u=0$, $a=-g=-10m{{s}^{-2}}$ and $s=-49m$.
Substitute these values in (i).
$-49=(0)t+\dfrac{1}{2}(-10){{t}^{2}}$
$\Rightarrow {{t}^{2}}=9.8$
$\Rightarrow t=\sqrt{9.8}=3.16s$
This means that the time taken to reach the ground is 3.16s.
Let the horizontal acceleration of the ball be ${{v}_{H}}$ and its vertical acceleration is ${{v}_{V}}$,
When we look at the figure we get that
$\tan \theta =\dfrac{{{v}_{V}}}{{{v}_{H}}}\\\ \Rightarrow \tan \theta =\dfrac{10}{4.9}\\\ \Rightarrow \tan \theta =2.04$
$\therefore\theta ={{\tan }^{-1}}\left( 2.04 \right)\approx {{64}^{\circ }}$.
Therefore, the angle made by the line joining initial and final position of the ball with the horizontal is almost equal to ${{64}^{\circ }}$, which is greater than ${{45}^{\circ }}$.

Hence, the correct options are A, C and D.

Note: Some students may think that the ball will travel in a parabolic path. The ball would have travelled in a curved path if the ball had some velocity at the time of release, similar to the case of a projectile motion.The projectile is any object thrown into space upon which the only acting force is gravity. In other words, the primary force acting on a projectile is gravity. This doesn’t necessarily mean that the other forces do not act on it, just that their effect is minimal compared to gravity. The path followed by a projectile is known as a trajectory.