Question

A ball is dropped from a height of 20m above the surface of a water in a lake. The refractive index of water is 4/3. A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant when the ball is 12.8m above the water surface, the fish sees the speed of the ball as-
a)9m/s
b)12m/s
c)16m/s
d)21.33m/s

Answer 1

We are asked basically to calculate the speed of the ball observed by the fish at instant when the ball is 12.8m above the surface of the lake. At every position of the ball with respect to the surface of the lake at any instant time, the fish will observe the ball to be at greater height than its actual height. Hence we will obtain the equation of the position of the ball with respect to the position of fish inside water and accordingly differentiate the equation to obtain the velocity of the ball observed by the fish.

Formula used:
$D=x+\mu h$
${{V}^{2}}-{{U}^{2}}=2gs$

Complete answer:

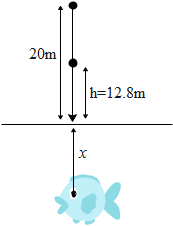
To begin with let us first determine the speed of the ball when it is above 12.8m from the surface of the water. Let us say a body free falls due to gravity where acceleration due to gravity is $g=10m{{s}^{-2}}$. Let the initial speed of the body be ‘U’. Then when it covers a distance of s meters than the velocity of the body at that point ‘V’ is given by,
${{V}^{2}}-{{U}^{2}}=2gs$
When the ball moves from 20 m to 12.8m above the surface of water, the distance covered by the ball is
$s=20-12.8=7.2m$. Hence from above equation the velocity of the ball at that point is,
$\begin{aligned} & {{V}^{2}}-{{U}^{2}}=2gs \\\ & \Rightarrow {{V}^{2}}-0=2\times 10\times 7.2 \\\ & \Rightarrow V=\sqrt{144}m{{s}^{-1}}=12m{{s}^{-1}} \\\ \end{aligned}$
Let us say the fish is at a distance x from the surface of the water. Hence the fish will see the ball slightly raised from the actual position of the ball. Let us say the actual position of the ball from the surface of the water is h and the refractive index of water is ($\mu$). Then the distance D from the fish to the apparent position of the ball is equal to,
$D=x+\mu h$
Differentiating this equation we get with respect to time we get
$\begin{aligned} & \dfrac{dD}{dt}=\dfrac{dx}{dt}+\mu \dfrac{dh}{dt}\text{, }\because \dfrac{dx}{dt}=0 \\\ & \Rightarrow \dfrac{dD}{dt}=\dfrac{4}{3}12m{{s}^{-1}}=16m{{s}^{-1}} \\\ \end{aligned}$
Hence the fish will observe the ball to have a velocity of 16 meter per second when it is 12.89m from the surface of the lake.

So, the correct answer is “Option C”.

Note:
In the above solution we have considered $\dfrac{dx}{dt}=0$ as the fish does not move with time. If the fish moves as well the velocity of the ball observed at the same instant of time will be different. It will be either greater or smaller than the above velocity seen depending on the relative motion between the two.