Question

A ball falls from height $h$. After $1\,s$, another ball falls freely from a point $25\,m$ below the point from when the first ball falls. Both of them reach the ground at the same time. The value of $h$ is
$A.\,{\text{ 1}}1.2{\text{ }}m$
$B.\,{\text{ 2}}1.2{\text{ }}m$
$C.\,{\text{ }}31.2{\text{ }}m$
$D.\,{\text{ 4}}1.2{\text{ }}m$

Answer 1

In order to solve the question, we will use the Newton’s second law of motion on both the ball on ball A we will use it to find the time of flight of ball A while that time of flight will be use to substitute while calculating the value of h by applying the formula on ball B hence we will get to the answer

Formula used:
Newton’s second law of motion
$s = ut + \dfrac{1}{2}a{t^2}$
Here, $s$ refers to displacement, $u$ refers to initial velocity, $a$ refers to acceleration and $t$ refers to time period.

Complete step by step answer:
In the question we are given A ball falls from height h. After 1s, another ball falls freely from a point 25m below the point from when the first ball falls. Both of then reach the ground at the same time and we have to find the value of $h$ is

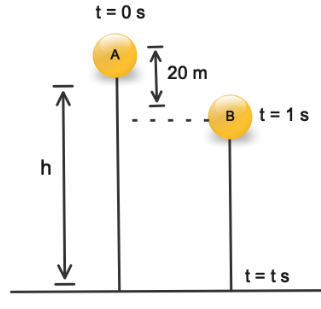
Let us take the time of flight of ball A = t s
Then, the time of flight of ball B = (t – 1) s
Now by applying Newton's second law we will find the value of $h$.
For Ball A: By using ball A we will find the time of flight of it.
Distance travelled = h
Time taken to travel distance = t s
Initial velocity = 0
Acceleration applied = g
Now applying the formula
$s = ut + \dfrac{1}{2}a{t^2}$
Substituting the value
$h = 0(t) + \dfrac{1}{2}g{t^2}$
Solving the equation for t
$t = \sqrt {\dfrac{{2h}}{g}} {\text{ }}s$

For Ball B: By using time of flight of ball A we will find the value of $h$.
Distance travelled = (h-20)
Time taken to travel distance = (t -1) s
Initial velocity = 0
Acceleration applied = g
Now applying the formula
$s = ut + \dfrac{1}{2}a{t^2}$
Substituting the value
$(h - 20) = 0(t - 1) + \dfrac{1}{2}g{(t - 1)^2}$
Solving the equation for h
$(h - 20) = \dfrac{1}{2}g{(t - 1)^2}$
Opening the square of time period
$h - 20 = \dfrac{{g{t^2}}}{2} + \dfrac{g}{2} - gt$
Substituting the time of flight of ball, A $t = \sqrt {\dfrac{{2h}}{g}} {\text{ }}s$
$h - 20 = \dfrac{g}{2}\left( {\dfrac{{2h}}{g}} \right) + \dfrac{g}{2} - g\sqrt {\dfrac{{2h}}{g}}$
$\Rightarrow h - 20 = h + \dfrac{g}{2} - g\sqrt {\dfrac{{2h}}{g}}$
h on both side will cut off
$h = \dfrac{{{{\left( {\dfrac{g}{2} + 20} \right)}^2}}}{{2g}}$
Now taking the value of $g = 10{\text{ m}}{{\text{s}}^{ - 2}}$
$h = \dfrac{{{{\left( {\dfrac{{10}}{2} + 20} \right)}^2}}}{{2 \times 10}}$
$\Rightarrow h = \dfrac{{{{\left( {25} \right)}^2}}}{{20}}$
$\therefore h = 31.25{\text{ }}m$

Hence, the correct option is C.

Note: Many of the students will make the mistake while calculation in ball b for finding h by substituting the value of t before opening the bracket of time of flight but first of fall we will open the bracket of time of flight then we have to substitute the value of t and value of g is taken $10{\text{ }}m{s^{ - 2}}$ instead of ${\text{9}}{\text{.8 }}m{s^{ - 2}}$ so as to make calculation easy as well as to match to the options.