Question

A ball falls from a height such that it strikes the floor of lift at 10 m/s. If lift is moving in the upward direction with a velocity 1 m/s, then velocity with which the ball rebounds after elastic collision will be
A. 11 m/s
B. 10 m/s
C. 12 m/s
D. 9 m/s

Answer 1

Two particles are moving in the same direction in a straight line with velocities $u_1$ and $u_2$ respectively. Before the collision their velocity of approach will be $({u_1} - {u_2})$
After collision velocity of the first particle and second particle are $v_1$ and $v_2$ respectively. Therefore, velocity of separation will be $({v_2} - {v_1})$.
Coefficient of restitution is the ratio of relative velocity of separation after collision to relative velocity of approach before collision.
Coefficient of restitution, $e = \dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}}$
For, elastic collision, $e = 1$.

Complete step by step answer:
Let us consider ball as particle 1 and lift as particle 2.
See the diagram before collision:

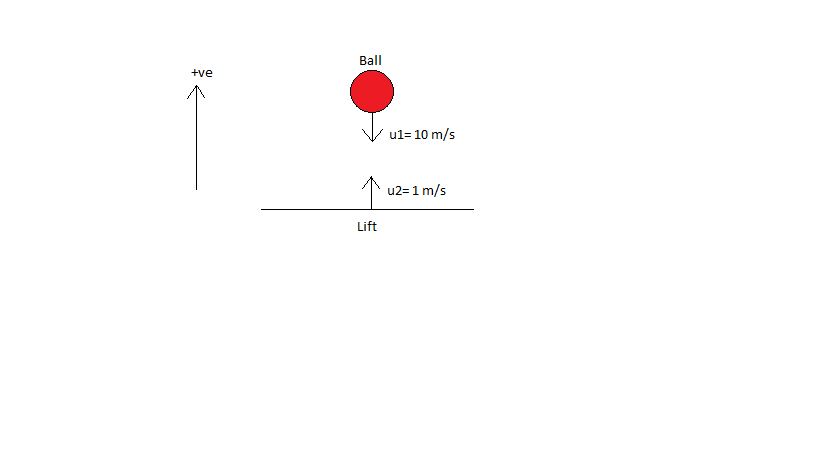
Taking upward direction as positive,
Velocity of ball before collision, ${u_1} = - 10$m/s
Velocity of lift before collision, ${u_2} = 1$m/s
Now, we should consider the situation after the collision.
After collision lift will continue it’s motion 1m/s upwards and the ball will rebound with a velocity, say $v_2$ in upward direction.
So, Velocity of lift after collision, ${v_2} = 1$m/s
Velocity of ball after collision be ${v_1}$m/s (let)
As it is an elastic collision, then$e = 1$.
We know, $e = \dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}}$
Now, putting the values,
$1 = \dfrac{{1 - {v_1}}}{{ - 10 - 1}}$
$\implies 1 - {v_1} = - 11$
$\therefore {v_1} = 11 + 1 = 12$m/s
So, Ball rebounds with 12m/s velocity upwards after elastic collision.

So, the correct answer is “Option C”.

Note:
We can take $e = 1$, when the collision is elastic. We can’t take $e = 1$for inelastic or partially elastic collision. For, perfectly inelastic collision, $e = 0$and for partially elastic collision $0 < e < 1$.