Question

A ball after falling from a height of $10m$ strikes the roof of a lift which is descending down with a velocity of $1m/s$. The recoil velocity of the ball will be:-
$A)\,8m/s$
$B)\,11m/s$
$C)\,12m/s$
$D)\,15m/s$

Answer 1

This situation can be considered to be a perfectly elastic collision between a body one of whose masses is negligible in comparison to the other. If both the bodies were moving in the same direction before collision, the final speed of the lighter body will be its original speed minus double the original speed of the heavier body.

Formula used:
$v=\sqrt{2gh}$

Complete answer:
This is a situation of an elastic collision between a much heavier body (the lift) and the much lighter body (the ball). So, we can use the formula for the final speed of a lighter body after it collides with a much heavier object moving in the same direction.
The final speed $v$ of a lighter body after it collides elastically with a much heavier body moving with a speed $U$ in the same direction is given by
$v=u-2U$ --(1)
Where $u$ is the speed of the lighter body before the collision.
The speed $v$ attained by a body when it is dropped from a height $h$ is given by
$v=\sqrt{2gh}$ --(2)
Where $g=9.8m/{{s}^{2}}$ is the acceleration due to gravity.
Now, let us analyze the question.

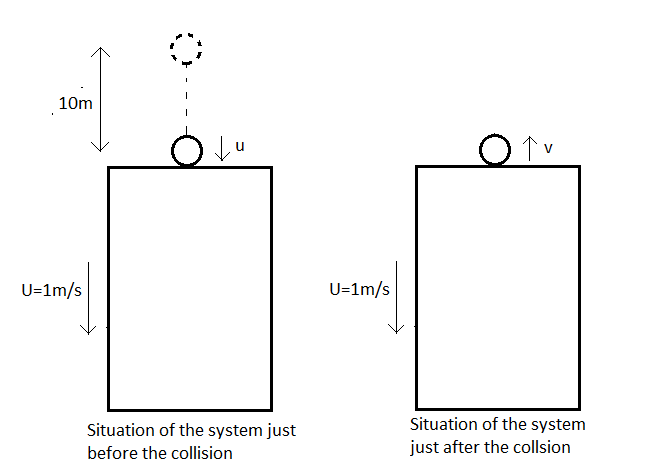
The height from which the ball drops is $h=10m$.
Let the speed of the ball just before the collision be $u$.
Let the rebound speed of the ball after the collision be $v$.
The speed of the lift is $U=1m/s$.
Now, using (1), we get
$u=\sqrt{2\times 9.8\times 10}=\sqrt{196}=14m/s$ --(3)
Also, using (2), we get
$v=u-2U$
Putting (3) in the above equation, we get
$v=14-\left( 2\times 1 \right)=14-2=12m/s$
Hence, we have got the rebound speed of the ball as $12m/s$.

So, the correct answer is “Option C”.

Note:
Students must note that the direction of the motion, that is, the sign of the speed is imperative in solving such elastic collision problems mathematically. For example, if the lift was moving in the opposite direction of the original direction of motion of the ball, then the final rebound speed of the ball will be the sum of the original speed of the ball and twice the speed of the lift, that is, then the equation would then have been $v=u+2U$ and the change in the direction of motion is represented in the change of sign of $U$.