Question

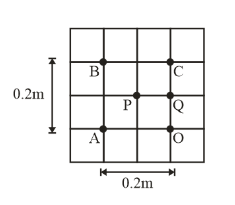
A, B, C, D, P and Q are points in a uniform electric field. The potentials at these points are $V(A) = 2r, V(P) = V(B) = V(D) = 5V, V(C) = 8V$. The electric field at P is

(A) $10V{m^{ - 1}}$ along PQ
(B) $15\sqrt 2 V{m^{ - 1}}$ along PA
(C) $5V{m^{ - 1}}$ along PC
(D) $5V{m^{ - 1}}$ along PA

Answer 1

In order to solve this problem, first we calculate the net potential at point P and then calculate the electric field at point P by using following formula –
$\vec E = - \dfrac{{dV}}{{dr}}$
Where $\vec E =$ electric field
$V =$ Electric potential

Complete step by step answer:
We know that the relation between electric field and electric potential is given as
$\vec E = - \dfrac{{dV}}{{dr}}$
In x-direction
${E_x} = - \dfrac{{dV}}{{dx}}$
According to diagram
$dx = 0.2m$
$dV = {V_0} - {V_A}$
So, ${E_x} = \dfrac{{ - ({V_0} - {V_A})}}{{0.2}}$
Given that $V(D) = 5V$
$V(A) = 2V$
So, ${E_x} = \dfrac{{ - (5 - 2)}}{{0.2}} = \dfrac{{ - 3}}{{0.2}}$
${E_x} = \dfrac{{ - 30}}{2} = - 15\dfrac{V}{m}$ …..(1)
In y-direction
${E_y} = - \dfrac{{dV}}{{dy}}$
According to diagram
$dy = 0.2m$
$dV = {V_B} - {V_A}$
So, ${E_y} = - \dfrac{{({V_B} - {V_A})}}{{0.2}}$
Given that $V(B) = 5V,V(A) = 2V$
${E_y} = \dfrac{{ - (5 - 2)}}{{0.2}} = \dfrac{{ - 3}}{{0.2}}$
${E_y} = \dfrac{{ - 30}}{2} = - 15\dfrac{V}{m}$ …..(2)
$\because \vec E = {E_x}\hat i + {E_y}\hat j$
So, $|\vec E| = \sqrt {E_x^2 + E_y^2}$
From equation 1 & 2
Electric field E at P is
$= \sqrt {{{( - 15)}^2} + {{( - 15)}^2}}$
$= \sqrt {2{{(15)}^2}}$
$= \sqrt 2 15 = 15\sqrt 2 \dfrac{V}{m}$
Hence, the electric field at point P is $15\sqrt 2 V{m^{ - 1}}$ along PA.

Note: In many cases potential is the function of x, y and z then electric field is given as
$\vec E = \dfrac{{ - \partial V}}{{\partial x}}\hat i - \dfrac{{\partial V}}{{\partial y}}\hat j - \dfrac{{\partial V}}{{\partial z}}\hat k$
Where ${E_x} = \dfrac{{ - \partial V}}{{\partial x}},{E_y} = - \dfrac{{\partial V}}{{\partial y}},{E_z} = \dfrac{{ - \partial V}}{{\partial z}}$