Question

A, B, C and D are four points such that AB $= m(2i - 6j + 2k),$ BC $= i + 2j$ and
CD $= n( - 6i + 15j - 3k)$ If AB and CD intersect at some point H, then
(This question has multiple correct options)
A. $m \geqslant \dfrac{1}{2}$
B. $n \geqslant \dfrac{1}{2}$
C.Area of $\Delta BCH = \dfrac{1}{{2}}\sqrt 6$
D.All of these

Answer 1

Hint : Here we will use the different concepts of the solutions of the equations, the cross-product of the vector equation and area of the triangle using the cross product of vectors. Substitute and simplify as per the required solution.

Complete step-by-step answer :

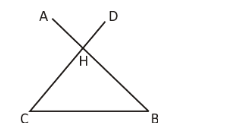
Given that lines AB and CD intersect at the point H and now connect the points C and B.
So, the triangle BCH is formed.
Also,
$\overrightarrow {AB} = m(2i - 6j + 2k),$
$\overrightarrow {BC} = i + 2j$ and
$\overrightarrow {CD} = n( - 6i + 15j - 3k).$
From the above figure, we can say that $\overrightarrow {HB} = x\overrightarrow {AB}$
Where, “x” lies between zero and one. Such that $0 < x < 1$
Similarly, $\overrightarrow {CH} = y\overrightarrow {CD}$
Now, in $\Delta CHB,$
$\Rightarrow \overrightarrow {CH} + \overrightarrow {HB} = \overrightarrow {CB}$
Place values from the given data –
$\Rightarrow yn( - 6i + 15j - 3k) + xm(2i - 6j + 2k) = - i - 2j$
Multiply the factors inside the bracket and simplify the above equations –
$\Rightarrow ( - 6yni + 15ynj - 3ynk) + (2xmi - 6xmj + 2xmk) = - i - 2j$
Make pair of terms with respect to the “i”, “j” and “k” terms –
$\Rightarrow \underline { - 6yni + 2xmi} + \underline {15ynj - 6xmj} \underline { - 3ynk + 2xmk} = - i - 2j$
Take common the respective terms –
$\Rightarrow i( - 6ny + 2mx) + j(15yn - 6x) + k( - 3yn + 2xm) = - i - 2j$
Now, compare the respective i,j and k terms on both the sides of the equation –
$\Rightarrow - 6ny + 2mx = - 1\,{\text{ }}....{\text{ (A)}} \\\ \Rightarrow 15yn - 6mx = - 2{\text{ }}....{\text{ (B)}} \\\ \Rightarrow ( - 3yn + 2xm) = 0{\text{ }}....{\text{ (C)}} \\\$
Simplify the equations to get the values of the terms “x” and “y”
Solve the equation (c)
$\Rightarrow ( - 3yn + 2xm) = 0{\text{ }} \\\ \Rightarrow 3yn = 2xm\;{\text{ }}....{\text{ (D)}} \\\$
Place the value of the equation (D) in the equation (A)
$\Rightarrow - 4mx + 2mx = 1\,{\text{ }}$
Simplify the equation –
$\Rightarrow 2mx = 1\,{\text{ }} \\\ \Rightarrow {\text{x = }}\dfrac{1}{{2m}} \\\$
Similarly place the above value in the equation (A)
$\Rightarrow - 6ny + 2mx = - 1$
$\Rightarrow - 6ny + 2m\left( {\dfrac{1}{{2m}}} \right) = - 1$
Like terms from the multiplicative and the division part cancel each other.
$\Rightarrow - 6ny + 1 = - 1$
When the term is moved from one side to another, sign also changes from negative to positive and vice-versa.
$\Rightarrow - 6ny = - 1 - 1 \\\ \Rightarrow - 6ny = - 2 \\\$
Minus sign cancel each other from both the sides of the equation, and make the unknown “y” the subject.
$\Rightarrow y = \dfrac{2}{{6n}} \\\ \Rightarrow y = \dfrac{1}{{3n}} \\\$
Because, we assume $0 < x < 1$ and $0 < y < 1$
$\Rightarrow 0 < \dfrac{1}{{2m}} < 1{\text{ and }}0 < \dfrac{1}{{3n}} < 1$
Simplification implies –
$\Rightarrow m > \dfrac{1}{2}{\text{ and n}} > \dfrac{1}{3}{\text{ }}....{\text{ (i)}}$
Now, the area of $\left| {\Delta CHB} \right| = \dfrac{1}{2}\left| {(\overrightarrow {HB} \times \overrightarrow {CH} )} \right|$ .... (i)
Now, $\overrightarrow {HB} = x\overrightarrow {AB}$
$\overrightarrow {HB} = xm(2i - 6j + 2k),$
Place the values $\Rightarrow 2mx = 1\,{\text{ }} \Rightarrow {\text{mx = }}\dfrac{1}{2}$
$\overrightarrow {HB} = \dfrac{1}{2}(2i - 6j + 2k) \\\ \overrightarrow {HB} = (i - 3j + k){\text{ }}....{\text{ (ii)}} \\\$
Similarly, $y\overrightarrow {CD} = yn( - 6i + 15j - 3k)$
Place the values - $yn = \dfrac{1}{3}$
$y\overrightarrow {CD} = \dfrac{1}{3}( - 6i + 15j - 3k) \\\ y\overrightarrow {CD} = ( - 2i + 5j - k){\text{ }}....{\text{ (iii)}} \\\$
Find the cross-product by using equations (ii) and (iii)
\overrightarrow {HB} \times \overrightarrow {CH} = \left| {\begin{array}{*{20}{c}} i&j;&k; \\\ 1&{ - 3}&1 \\\ { - 2}&5&{ - 1} \end{array}} \right|
Expand the determinant-
$\overrightarrow {HB} \times \overrightarrow {CH} = i[( - 3)( - 1) - 5] - j[(1)( - 1) - ( - 2)(1) + k[(1)(5) - ( - 3)( - 2)]$
Simplify the above equation –
$\overrightarrow {HB} \times \overrightarrow {CH} = i(3 - 5) - j( - 1 + 2) + k(5 - 6) \\\ \overrightarrow {HB} \times \overrightarrow {CH} = - 2i - j - k \\\$
Find the magnitude –
$\left| {\overrightarrow {HB} \times \overrightarrow {CH} } \right| = \left| { - 2i - j - k} \right| \\\ \Rightarrow \left| {\overrightarrow {HB} \times \overrightarrow {CH} } \right| = \sqrt {{{( - 2)}^2} + {{( - 1)}^2} + {{( - 1)}^2}} \\\$
Square of negative terms gives the positive terms-
$\Rightarrow \left| {\overrightarrow {HB} \times \overrightarrow {CH} } \right| = \sqrt {4 + 1 + 1} = \sqrt 6$
Now, place the above value in the equation (i)
$\left| {\Delta CHB} \right| = \dfrac{1}{2}\left| {(\overrightarrow {HB} \times \overrightarrow {CH} )} \right| \\\ \Rightarrow \left| {\Delta CHB} \right| = \dfrac{1}{2}(\sqrt 6 ) \\\$
Simplify the above equation –
$\Rightarrow \left| {\Delta CHB} \right| = \dfrac{{\sqrt 6 }}{2}$
Hence, from the given multiple choices- all the given options are the correct answer.
So, the correct answer is “Option D”.

Note : Always remember the properties of the cross-product and expansion of the determinant and simplify taking care of the positive and the negative sign. Also, remember the square and square-roots and its simplification for the efficient and accurate solution.