Solveeit Logo
Login

Question

Question: A, B and C represents switches in ‘on’ position and A’, B’ and C’ represents them in ‘off’ position....

A, B and C represents switches in ‘on’ position and A’, B’ and C’ represents them in ‘off’ position. Construct a switching circuit representing the polynomial ABC+AB′C+A′B′CABC + AB'C + A'B'C. Using Boolean algebra, prove that the given polynomial can be simplified to C(A+B′)C\left( {A + B'} \right). Construct an equivalent switching circuit.

Explanation

Solution

Hint: Use the property of Boolean algebra which are A.A = A,{\text{ }}A.A' = 0,{\text{ }}A\left( {1 + B'} \right) = A,{\text{ & }}\left( {A + A'} \right) = 1 for solving this problem.

Complete step-by-step answer:
Given polynomial is ABC+AB′C+A′B′CABC + AB'C + A'B'C switching circuit representing the given polynomial is shown in figure (1), where A, B and C represents switches in ‘on’ position and A’, B’ and C’ represents them in ‘off’ position

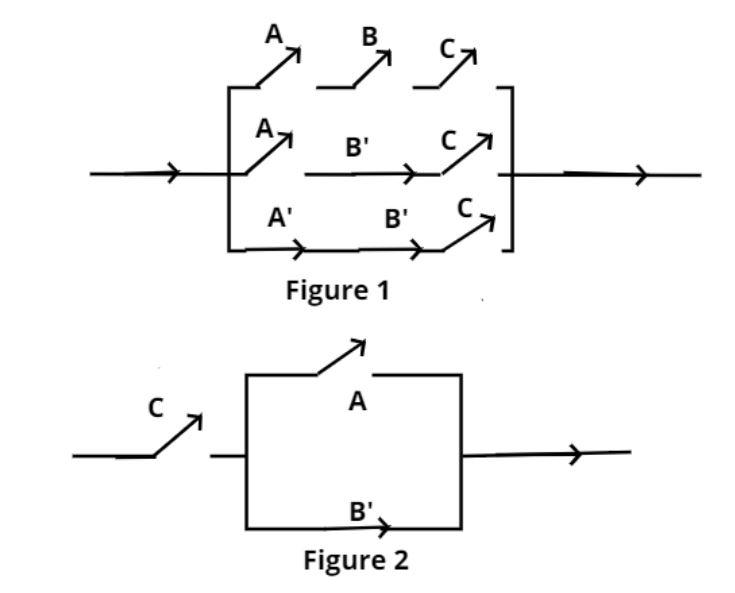
Now we have to prove that
ABC+AB′C+A′B′C=C(A+B′)ABC + AB'C + A'B'C = C\left( {A + B'} \right)
Consider L.H.S
ABC+AB′C+A′B′CABC + AB'C + A'B'C
Take AC common from first two terms
⇒AC(B+B′)+A′B′C\Rightarrow AC\left( {B + B'} \right) + A'B'C
As we know in Boolean algebra value of (B+B′)\left( {B + B'} \right) is equal to one
⇒AC(B+B′)+A′B′C=AC+A′B′C\Rightarrow AC\left( {B + B'} \right) + A'B'C = AC + A'B'C
Now take C as common
⇒AC+A′B′C\Rightarrow AC + A'B'C = C(A+A′B′).............(1)C\left( {A + A'B'} \right).............\left( 1 \right)
Now (A+A′B′)\left( {A + A'B'} \right) is written as(A+A′)(A+B′)\left( {A + A'} \right)\left( {A + B'} \right), property of Boolean algebra.
Because we know in Boolean algebra the value of A.A = A,{\text{ }}A.A' = 0,{\text{ & }}A\left( {1 + B'} \right) = A
So,
(A+A′)(A+B′)=A.A+A.B′+A.A′+A′B′ =A+AB′+0+A′B′ =A(1+B′)+A′B′=A+A′B′  \left( {A + A'} \right)\left( {A + B'} \right) = A.A + A.B' + A.A' + A'B' \\\ = A + AB' + 0 + A'B' \\\ = A\left( {1 + B'} \right) + A'B' = A + A'B' \\\
Therefore
(A+A′B′)=(A+A′)(A+B′)\left( {A + A'B'} \right) = \left( {A + A'} \right)\left( {A + B'} \right)
Therefore from equation (1)
⇒ABC+AB′C+A′B′C=C(A+A′B′)=C(A+A′)(A+B′)\Rightarrow ABC + AB'C + A'B'C = C\left( {A + A'B'} \right) = C\left( {A + A'} \right)\left( {A + B'} \right)
Now as we know in Boolean algebra value of (A+A′)\left( {A + A'} \right) is equal to one
⇒ABC+AB′C+A′B′C=C(A+B′)\Rightarrow ABC + AB'C + A'B'C = C\left( {A + B'} \right)
=R.H.S
Hence Proved.

And the equivalent representation is shown in figure (2), where A, B and C represents switches in ‘on’ position and A’, B’ and C’ represents them in ‘off’ position.

Note: Whenever we face such types of questions always remember some of the basic properties of the Boolean algebra which is stated above then using these properties simplify the given polynomial, we will get the required answer.