Question

A, B and C are three collinear points. The Coordinates of A and B are $\left( {3,4} \right)$ and $\left( {7,7} \right)$ respectively and $AC = 10$ Units. Find the sum of coordinates of C.

Answer 1

We use the midpoint formula to solve this problem and first find out the coordinates of C and their sum.

Formula Used:
Coordinates of the middle point G of two points $M\left( {x,y} \right)$ and $N\left( {a,b} \right)$ which lie of the same line is given by $G\left( {\dfrac{{x + a}}{2},\dfrac{{y + b}}{2}} \right)$.

Complete step-by-step answer:
A,B and C collinear points, as they lie on the same line.

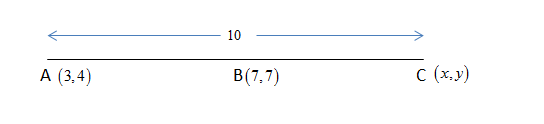
Let the coordinate of point C be $\left( {x,y} \right)$
Distance formula between two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ , $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Using the distance formula between two points $A\left( {3,4} \right)$ and $B\left( {7,7} \right)$

$${d_{AB}} = \sqrt {{{\left( {7 - 3} \right)}^2} + {{\left( {7 - 4} \right)}^2}} \\\ {d_{AB}} = \sqrt {16 + 9} \\\ {d_{AB}} = 5 \\\$$

The distance between the points A and B is 5 units. The distance between B and C is given by
${d_{BC}} = {d_{AC}} - {d_{AB}} \\\ {d_{BC}} = 10 - 5 \\\ {d_{BC}} = 5 \\\$
It means that B is the mid-point of A and C.
The coordinates of the mid-point G, lying between the two points $M\left( {x,y} \right)$ and $N\left( {a,b} \right)$ , is given by $G\left( {\dfrac{{x + a}}{2},\dfrac{{y + b}}{2}} \right)$.
Using it, find the coordinates of point B.
Coordinates of $A\left( {3,4} \right)$ and $C\left( {x,y} \right)$
$B\left( {\dfrac{{3 + x}}{2},\dfrac{{4 + y}}{2}} \right)$
But the coordinates of B is $\left( {7,7} \right)$ . Equate the X-Coordinate and Y-Coordinate of $B\left( {\dfrac{{3 + x}}{2},\dfrac{{4 + y}}{2}} \right)$ and $B\left( {7,7} \right)$ to calculate the coordinates of $C\left( {x,y} \right)$
$\dfrac{{3 + x}}{2} = 7 \\\ x = 11 \\\$
Also,
$\dfrac{{4 + y}}{2} = 7 \\\ y = 10 \\\$
The coordinates of point C is $\left( {11,10} \right)$ .
The sum of coordinates of point C,
$S = 11 + 10 \\\ S = 21 \\\$
Thus, the sum of the coordinates of point C is $S = 21$

Note: Collinear points are those points which lie on the same line. For A, B, and C to be collinear, the area of the triangle should be equal to 0.
Important concept and formulas to be remembered are
The distance between two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ , $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
The midpoint of two points, all lying on the same line is calculated as , $G\left( {\dfrac{{x + a}}{2},\dfrac{{y + b}}{2}} \right)$ where two points are $M\left( {x,y} \right)$ and $N\left( {a,b} \right)$.