Question

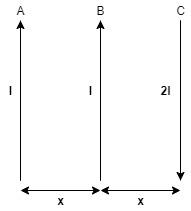
A, B and C are parallel conductors of lengths as shown in the figure carrying currents $I$, $I$ and $2I$ respectively. The distance between $A$ and $B$ is $x$. The distance between $B$ and $C$ is also $x$. ${F_1}$ is the force exerted by $B$ on $A$. ${F_2}$ is the force exerted by $C$ on $A$. Choose the correct answer.

A) ${F_1} = 2{F_2}$
B) ${F_2} = 2{F_1}$
C) ${F_1} = {F_2}$
D) ${F_1} = - {F_2}$

Answer 1

Electric current produces magnetic field. Then these magnetic fields produced by the current-carrying wires will exert force upon the current-carrying wires. Here you need to identify those magnetic fields and calculate the forces accordingly. You also need to carefully note the directions of the magnetic fields and the forces.

Formulae Used:
The magnetic field $B$ due to a current carrying wire carrying current $I$ at a distance of $x$ apart is
$B = \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{I}{x}$
where ${\mu _0}$ is the permeability of vacuum.
The force exerted $F$ on a current carrying wire of length $l$ carrying $I$ current is
$F = BIl$

Complete step by step answer:
Given:
The current carrying wire $A$ of length $l$ is carrying a current $I$ in upward direction.
The current carrying wire $B$ of length $l$ is carrying a current $I$ in upward direction.
The current carrying wire $C$ of length $2l$ is carrying a current $2I$ in downward direction.
${F_1}$ is the force exerted by $B$ on $A$ and ${F_2}$ is the force exerted by $C$ on $A$.
To get: The relation between ${F_1}$ and ${F_2}$.
Step 1:
Current carrying wire $A$ and $B$ are carrying current in the parallel direction.
Hence from right hand rule you can get that the magnetic field ${B_{BA}}$ due to $B$on $A$ will be inward-directed to the plane.
You can calculate the magnetic field ${B_{BA}}$ from eq (1) when the distance between $A$ and $B$ is $x$ and $B$ carrying current $I$.
${B_{BA}} = \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{I}{x}$
Step 2:
Current carrying wire $C$ and $A$ are carrying current in anti-parallel direction.
Hence from the right-hand rule, you can get that the magnetic field ${B_{CA}}$ due to $C$ on $A$ will be inward-directed to the plane.
You can calculate the magnetic field ${B_{CA}}$ from eq (1) when, the distance between $C$ and $A$ is $\left( {x + x} \right)$ and $C$ carrying current $2I$.
${B_{CA}} = - \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{{2I}}{{(x + x)}} \\\ \Rightarrow {B_{CA}} = - \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{{2I}}{{2x}} \\\ \therefore {B_{CA}} = - \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{I}{x} \\\$
Step 3:
The force exerted on $A$ due to the magnetic field ${B_{BA}}$ is
${F_1} = BIl \\\ = {B_{BA}}Il \\\ = \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{I}{x}Il \\\ = \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{{{I^2}l}}{x} \\\$
Step 4:
The force exerted on $A$ due to the magnetic field ${B_{CA}}$ is
${F_2} = BIl \\\ = {B_{CA}}Il \\\ = - \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{I}{x}Il \\\ = - \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{{{I^2}l}}{x} \\\$
Hence, comparing the two forces you can get
${F_1} = - {F_2}$

The correct answer is (D) ${F_1} = - {F_2}$.

Note:
The direction of the current being different in the cases of $B$ and $C$, the produced magnetic fields are of different directions. These magnetic fields exert force on $A$ along the perpendicular direction of the respective magnetic fields and hence they are of the opposite direction. Thus, you need to be careful while dealing with directions. Again, one important point where many students fail is the in the eq (2) the length and the current is of the wire itself on which the force is being exerted.