Solveeit Logo
Login

Question

Question: a \> b \> 0 and f(q) =\(\frac { \left( a ^ { 2 } - b ^ { 2 } \right) \cos \theta } { a - b \sin \the...

a > b > 0 and f(q) =(a2−b2)cos⁡θa−bsin⁡θ\frac { \left( a ^ { 2 } - b ^ { 2 } \right) \cos \theta } { a - b \sin \theta }, then the maximum value of f(q) is

A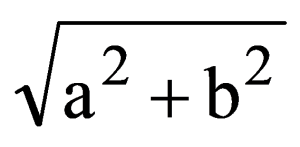
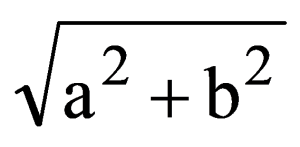
B

a2−b2\sqrt { a ^ { 2 } - b ^ { 2 } }

C

a – b

D

) a + b

Answer

a2−b2\sqrt { a ^ { 2 } - b ^ { 2 } }

Explanation

Solution

f(q) = (a2−b2)cos⁡θa−bsin⁡θ\frac { \left( a ^ { 2 } - b ^ { 2 } \right) \cos \theta } { a - b \sin \theta }=

f(q) = a2−b2 h(θ)\frac { \mathrm { a } ^ { 2 } - \mathrm { b } ^ { 2 } } { \mathrm {~h} ( \theta ) } , h(q) = a sec q – b tan q

f(q) is maximum and minimum according as h(q) is min. or max. respectively

h(q) = a sec q – b tan q

h'(q) = a sec q tan q – b sec2 q

for max. and min. of h(q) put h'(q) = 0

sec q (a tan q – b sec q) = 0

sin q = b/a .........(1) as [sec q ¹ 0]

h"(q) = sec q tan q (a tanq – b secq)

+ (a sec2q – b secq tan q) secq

= a sec3q + a sec q tan2q – 2b sec2q tan q

h"q = a+asin⁡2θ−2bsin⁡θcos⁡3θ\frac { a + a \sin ^ { 2 } \theta - 2 b \sin \theta } { \cos ^ { 3 } \theta }

= a+ab2/a2−2b⋅b/acos⁡3θ\frac { a + a b ^ { 2 } / a ^ { 2 } - 2 b \cdot b / a } { \cos ^ { 3 } \theta }

= a2−b2acos⁡3θ\frac { a ^ { 2 } - b ^ { 2 } } { a \cos ^ { 3 } \theta } > 0

{sin⁡θ=b/aa>b>0 and sin⁡θ=ba\left\{ \begin{array} { c } \sin \theta = b / a \\ a > b > 0 \text { and } \sin \theta = \frac { b } { a } \end{array} \right. is +ve

So, h(q) is minimum when sin q =

f(q) is maximum when sin q = ba\frac { \mathrm { b } } { \mathrm { a } }

max. f(q) =

Ž (a2−b2)(a2−b2)(a2−b2)\frac { \left( a ^ { 2 } - b ^ { 2 } \right) \left( \sqrt { a ^ { 2 } - b ^ { 2 } } \right) } { \left( a ^ { 2 } - b ^ { 2 } \right) }

max. f(q) = a2−b2\sqrt { a ^ { 2 } - b ^ { 2 } }