Question

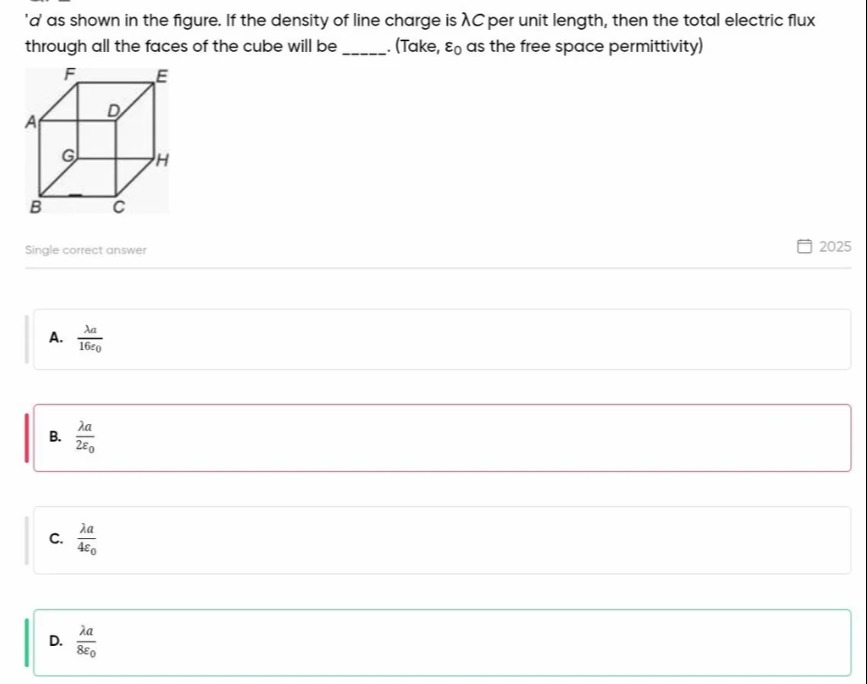
a' as shown in the figure. If the density of line charge is $\lambda$C per unit length, then the total electric flux through all the faces of the cube will be ________. (Take, $\epsilon_0$ as the free space permittivity)

• A. $\frac{\lambda a}{16\epsilon_0}$
• B. $\frac{\lambda a}{2\epsilon_0}$
• C. $\frac{\lambda a}{4\epsilon_0}$
• D. $\frac{\lambda a}{8\epsilon_0}$

Answer 1

Answer: (C)

$\frac{\lambda a}{4\epsilon_0}$

Answer 2

The problem asks for the total electric flux through all the faces of a cube of side length 'a' when a line charge of linear density $\lambda$ is placed along one of its edges, say BG. The length of the edge is 'a', so the total charge on the edge is $Q = \lambda a$.

According to Gauss's Law, the total electric flux through a closed surface is given by $\Phi = \frac{Q_{enclosed}}{\epsilon_0}$, where $Q_{enclosed}$ is the net charge enclosed by the surface.

In this case, the line charge is placed along an edge of the cube. When a charge distribution is on the boundary of the Gaussian surface, the charge enclosed by the surface is only a fraction of the total charge. For a line charge along an edge of a cube, the edge is shared by 4 identical cubes that meet at that edge.

Consider the edge BG. If we place 4 identical cubes such that they all share this edge, then the line charge along BG is effectively inside the combined volume of these 4 cubes. The total charge on the edge is $\lambda a$. By symmetry, the electric flux originating from this line charge will be distributed equally among the 4 cubes.

The total flux originating from the line charge of length 'a' with density $\lambda$ is $\frac{\lambda a}{\epsilon_0}$. Since this line charge is shared by 4 identical cubes when placed along an edge, the charge effectively enclosed by one cube is $\frac{1}{4}$ of the total charge, if we consider the contribution to the flux through one cube. Therefore, the total electric flux through the faces of the given cube is $\frac{1}{4} \times \frac{\text{Total charge}}{\epsilon_0} = \frac{1}{4} \times \frac{\lambda a}{\epsilon_0} = \frac{\lambda a}{4\epsilon_0}$.

This result can be understood by considering how many identical cubes are needed to make the edge an internal line segment. If we place 4 cubes around the edge, the edge becomes an internal edge for the combined structure. Thus, the flux through one cube is 1/4 of the total flux from the line charge.