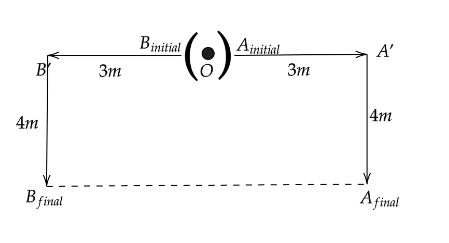
Question

$A$ and $B$ start from a point in opposite directions, and both travel $3$ meters (m). Then, both turn towards their, and travel another $4\,m$. What is the distance between $A$ and $B$ now?
A. $8\,m$
B. $9\,m$
C. $10\,m$
D. $11\,m$

Answer 1

First draw a rough diagram of two particles moving as per the given statement. Then join the final distance with the starting point. Now using pythagoras formula for two different points we can find the distance from its initial point, then on adding both of them we can find the distance between $A$ and $B$.

Complete step by step answer:
As per the problem we have A and B which start from a point in opposite directions, and both travel $3$ meters (m). Then, both turn towards their, and travel another $4\,m$.Now we have to calculate the distance between A and B.

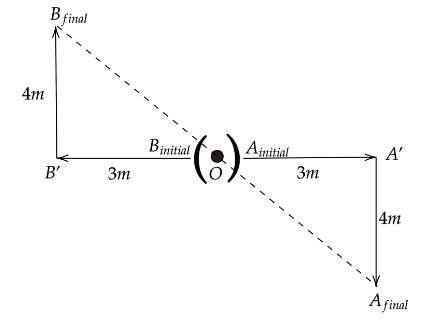
Here $o$ is the starting point of both A and B. When both move in opposite directions from the starting point they reach at A’ and B’ respectively. Then both turn their right and move to a certain distance and reach $Afinal\,and\,Bfinal$ respectively. Now join both the final points with their starting point.

Now using pythagoras formula separately on two triangles we will get,
In $\vartriangle OB'B_{final}$ we will get,
${\left( {OB'} \right)^2} + {\left( {B'B_{final}} \right)^2} = {\left( {OB_{final}} \right)^2}$
Now putting the values as per the figure we will get,
${\left( {3m} \right)^2} + {\left( {4m} \right)^2} = {\left( {OB_{final}} \right)^2}$
Now on further solving we will get,
$OB_{final} = 5m$

Similarly,
In $\vartriangle OA'A_{final}$ we will get,
${\left( {OA'} \right)^2} + {\left( {A'A_{final}} \right)^2} = {\left( {OA_{final}} \right)^2}$
Now putting the values as per the figure we will get,
${\left( {3m} \right)^2} + {\left( {4m} \right)^2} = {\left( {OA_{final}} \right)^2}$
Now on further solving we will get,
$OAfinal = 5m$
Now the distance between A and B is,
$A_{final}B_{final} = OA_{final} + OB_{final} \\\ \Rightarrow A_{final}B_{final}= 5m + 5m \\\ \therefore A_{final}B_{final}= 10\,m$

Therefore the correct option is $\left( C \right)$.

Note: While solving this type of problem it is necessary to draw a rough diagram to solve the problem easily. Keep in mind when you make the diagram as both the particles are moving in opposite directions their right turns are also opposite to each other. If we take the right turn in both cases in the same direction then your solution will be incorrect and you will get the solution as $6m$. Wrong diagram: