Solveeit Logo
Login

Question

Question: A and B are two points on a uniform ring of resistance \(R\). The \(\angle ACB=\theta \), where C is...

A and B are two points on a uniform ring of resistance RR. The ∠ACB=θ\angle ACB=\theta , where C is the centre of the ring. The equivalent resistance between A and B is:
(A). Rθ(2π−θ)4π2\dfrac{R\theta (2\pi -\theta )}{4{{\pi }^{2}}}
(B). R(1−θ2π)R\left( 1-\dfrac{\theta }{2\pi } \right)
(C). Rθ2π\dfrac{R\theta }{2\pi }
(D). Rθ(2π−θ)4π\dfrac{R\theta (2\pi -\theta )}{4\pi }

Explanation

Solution

A ring has uniform resistance as we divide the ring into parts by the points A and B, its length changes and hence its resistance depends on the length. Calculating resistance per unit length, we can use it to calculate the resistance of an individual part of the ring. Apply the right combination to the resistance and calculate the equivalent resistance accordingly.
Formulas used:
R′=R2πrR'=\dfrac{R}{2\pi r}
R′′=R1×R2R1+R2R''=\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}

Complete step-by-step solution:

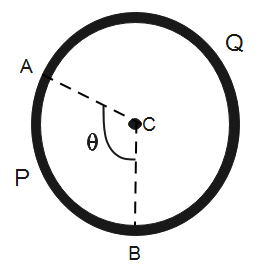
Given that the ring has a uniform resistance RR. Let rr be the radius of the ring, then the resistance per unit length will be-
R′=R2πrR'=\dfrac{R}{2\pi r} - (1)
Here, R′R' is the resistance per unit length of the ring
2πr2\pi r is the circumference or total length of the ring
The length of the arc APB will be-
l=rθl=r\theta - (2)
Here, θ\theta is the given angle ∠ACB\angle ACB
The length of the arc AQB will be-
l′=r(2π−θ)l'=r(2\pi -\theta ) - (3)
The resistance of each arc will be the product of length of arc and the resistance per unit length. Therefore, the resistance of APB will be-
R1=R2πr×rθ ⇒R1=Rθ2π \begin{aligned} & {{R}_{1}}=\dfrac{R}{2\pi r}\times r\theta \\\ & \Rightarrow {{R}_{1}}=\dfrac{R\theta }{2\pi } \\\ \end{aligned}
Therefore, the resistance of APB will be Rθ2π\dfrac{R\theta }{2\pi }.
From eq (1) and eq (3), the resistance of AQB will be-
R2=R2πrr(2π−θ) ⇒R2=R(2π−θ)2π \begin{aligned} & {{R}_{2}}=\dfrac{R}{2\pi r}r(2\pi -\theta ) \\\ & \Rightarrow {{R}_{2}}=\dfrac{R(2\pi -\theta )}{2\pi } \\\ \end{aligned}
Therefore, the resistance of AQB will be R(2π−θ)2π\dfrac{R(2\pi -\theta )}{2\pi }.
Both arcs APB and AQB are connected between two points AB and hence are connected in parallel. Therefore, their equivalent resistance will be-
R′′=R1×R2R1+R2R''=\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}
Substituting the value of R1{{R}_{1}} and R2{{R}_{2}} in the above equation, we get,
R′′=Rθ2π×R(2π−θ)2πRθ2π+R(2π−θ)2π ⇒R′′=Rθ(2π−θ)4π2 \begin{aligned} & R''=\dfrac{\dfrac{R\theta }{2\pi }\times \dfrac{R(2\pi -\theta )}{2\pi }}{\dfrac{R\theta }{2\pi }+\dfrac{R(2\pi -\theta )}{2\pi }} \\\ & \Rightarrow R''=\dfrac{R\theta (2\pi -\theta )}{4{{\pi }^{2}}} \\\ \end{aligned}
Therefore, the equivalent resistance between points A and B is Rθ(2π−θ)4π2\dfrac{R\theta (2\pi -\theta )}{4{{\pi }^{2}}}. Hence, the correct option is (A).

Note: In parallel combination, the voltage is the same. For resistors connected in parallel, the inverse of equivalent resistance is equal to the sum of inverse of all resistances. The resistance of a material is inversely proportional to its area of cross section and directly proportional to its length.