Question

A and B are two given like parallel forces. A couple of moments H lies in a plane of A and B and it is contained with them. The resultant of A and B after combining is displaced through a certain distance is,
$\begin{aligned} & A.\dfrac{2H}{A-B} \\\ & B.\dfrac{H}{A+B} \\\ & C.\dfrac{H}{2\left( A+B \right)} \\\ & D.\dfrac{H}{\left( A-B \right)} \\\ \end{aligned}$

Answer 1

A couple is dual equal forces which are acting in an opposite direction on an object but not through the similar point so they produce a turning effect. The moment or torque of a couple is given by multiplying the size of one of the forces we take by the perpendicular distance in between the two forces.

Complete step-by-step answer:

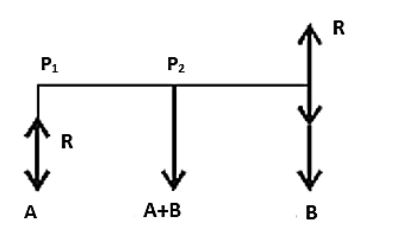
First of all let us discuss the moment of the couple in detail. It is actually the rotating ability of a couple. Moment of a couple is described as the product of one of the forces forming the couple and arm of the couple.
That is moment of couple can be written as,
Moment of a couple =Magnitude of either of the force × Arm of the couple.
Here it is given that A and B are the two parallel forces. A couple of moments $H$ is lying in the Plane of A and B and it is contained with them.
And it is also mentioned that the resultant of A and B after combining them is moved a distance of $d$
Therefore we can write that,
$\left( A+B \right)d=H$
Rearranging this will result in,
$d=\dfrac{H}{\left( A+B \right)}$

So, the correct answer is “Option B”.

Note: SI unit of moment of the couple is Newton metre abbreviated as $Nm$. When a body is rotating, the movement of the couple will be lying along the axis of rotation. To balance a couple, some other equal and also opposite couple is needed in the same plane. Moment of the couple is a positive value for the anti-clockwise rotation of the object. Moment of the couple becomes negative for the clockwise rotation of an object.