Question

A and B are two concentric spheres. If A is given a charge $Q$ while B is earthed as shown in figure:

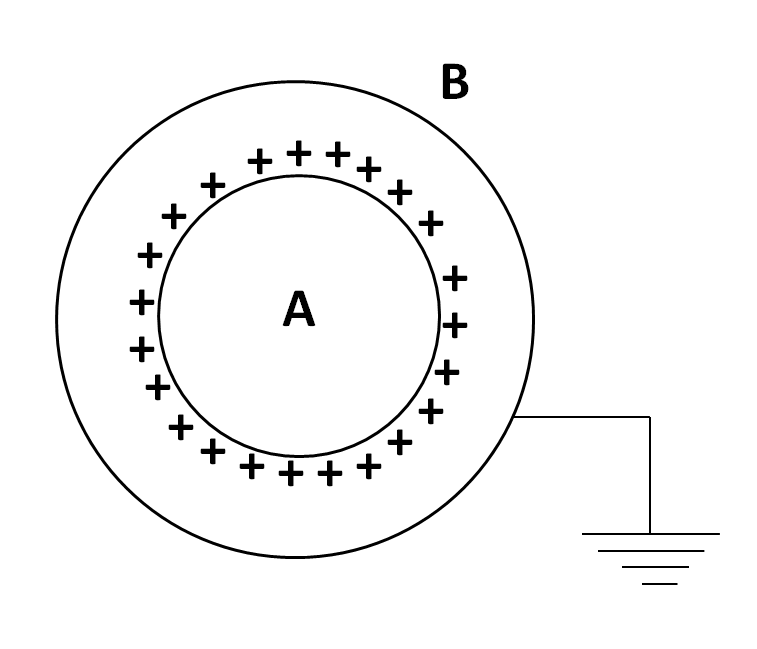
(A) The charge density of A and B are same
(B) The field inside and outside A is zero
(C) The field between A and B is not zero
(D) The field inside and outside B is zero

Answer 1

To solve this question, we need to use the Gauss theorem for determining the electric fields in different regions. We have to choose suitable symmetric Gaussian surfaces for the different regions. From there we can find the electric field or the charge density.

Formula Used: The formula used to solve this question is given by
$\int {EdS} = \dfrac{{{q_{enc}}}}{{{\varepsilon _0}}}$, here $E$ is the electric field, $dS$ is the elementary area of the Gaussian surface, and ${q_{enc}}$is the charge enclosed by the Gaussian surface.

Complete step-by-step solution:
The positive charge $Q$ present on the inner sphere A, will get uniformly distributed on its outside surface. It will attract the negatively charged electrons from the inner surface of the outer sphere B. So, negative charge, equal and opposite to $+ Q$ will come on the inner surface of the sphere B. Also, the corresponding positive charge created on the outer surface of the sphere B. As the outside surface of B is earthed, so all the charge will be transferred to the ground and hence net charge on the outside surface of the sphere B will become zero. So the charge distribution can be shown as the figure below.

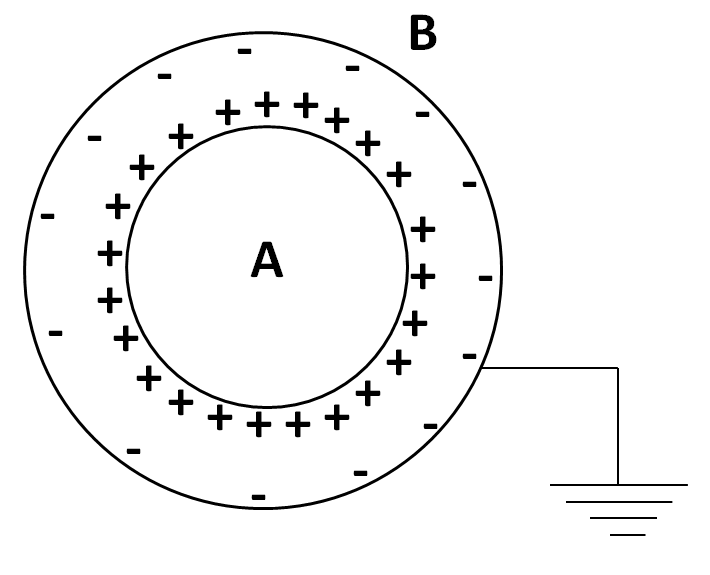
Now, the charge on the sphere B is equal and opposite to the charge on the sphere A and it is given by
${q_B} = - {q_A}$
${q_B} = - Q$
We know that the charge density is given by
$\sigma = \dfrac{q}{A}$
The surface area of a sphere is given by,
$A = 4\pi {r^2}$
So we get
$\sigma = \dfrac{q}{{4\pi {r^2}}}$
As the charge is equal on both the spheres, so we have the charge density as
$\sigma \propto \dfrac{1}{{{r^2}}}$
Since the radius of sphere A is less than that of sphere B, so its charge density will be less.
So the option A is incorrect.
Now, from Gauss theorem we know that
$\int {EdS} = \dfrac{{{q_{enc}}}}{{{\varepsilon _0}}}$ (1)
For the electric field inside A, we draw a Gaussian surface inside the sphere A, as shown below.

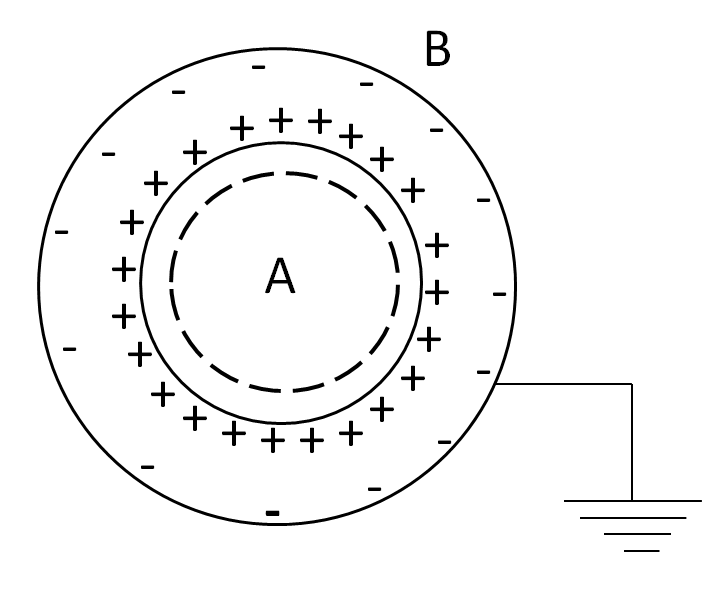
As the charge enclosed by the Gaussian surface is zero, so from (1) we have
$\int {EdS} = 0$
Which gives us
$E = 0$
So the electric field inside the sphere A is equal to zero.
Now, for the electric field between A and B, we consider a Gaussian surface as shown.

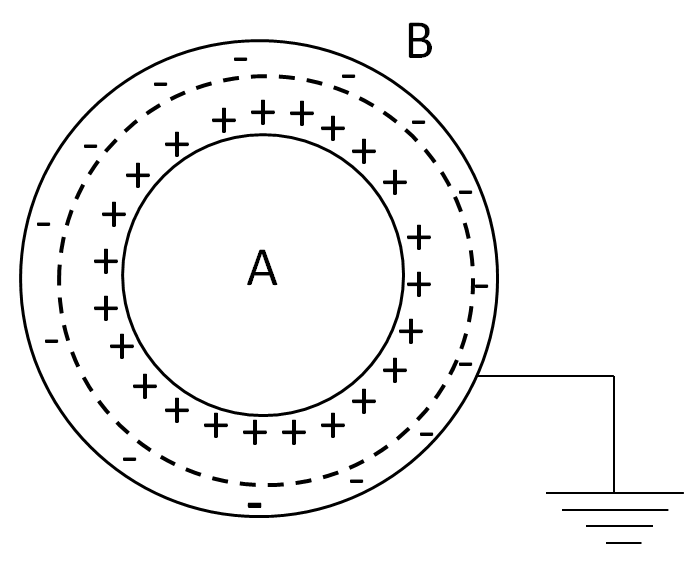
As we can see that the charge enclosed by the Gaussian surface is equal to $Q$. So from (1) we have
$\int {EdS} = \dfrac{Q}{{{\varepsilon _0}}}$
So, clearly the electric field between A and B is not zero.
So the option C is correct.
Finally, for the field outside the sphere B, we consider a Gaussian surface as shown below.

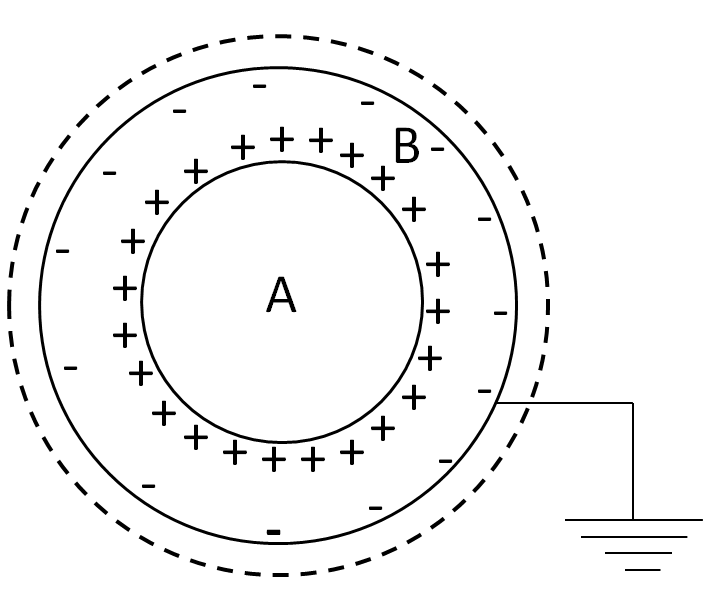
As we can see in the above figure, the charge enclosed by the Gaussian surface is
${q_{enc}} = Q - Q = 0$
So from (1) we have
$\int {EdS} = 0$
Which gives us,
$E = 0$
So the electric field outside the sphere B is equal to zero.
Thus, the electric field is zero inside A, non-zero outside A and inside B and is zero outside B. The outside region for the sphere A is divided into two regions. One is between A and B, and the other is outside B. As we have shown above that the electric field is not zero for the former, while it is zero for the latter. So option B is incorrect.
Also, the region inside the sphere B is divided into two parts; the region between A and B and the region inside A. As shown above, the electric field is not zero for the first part, while it is zero for the second part.
So the option D is also incorrect.

Hence, the only correct option is C.

Note: As we are asked to find out whether the electric field is zero or not in the above mentioned regions, there is no need to calculate the exact value of the electric field. So just by calculating whether the charge enclosed by the Gaussian surface is non-zero, we can find if it has a non-zero electric field.