Question

a and b are the angles made by a vector, from positive x and positive y axes, respectively. Which set of a and b is not possible?

$A.\,45{}^\circ ,\,60{}^\circ$
$B.\,30{}^\circ ,\,60{}^\circ$
$C.\,60{}^\circ ,\,60{}^\circ$
$D.\,30{}^\circ ,\,45{}^\circ$

Answer 1

Using the basic properties of the vectors and the direction cosines, this problem can be solved. The limits are given in the statement, like, the angles made by a vector from the positive x-axis and the positive y-axis should be taken into consideration. As the trick to solve this type of question lies in the given question statement itself.

Formula used:
${{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =1$

Complete step by step answer:
Consider a vector in 3D space.

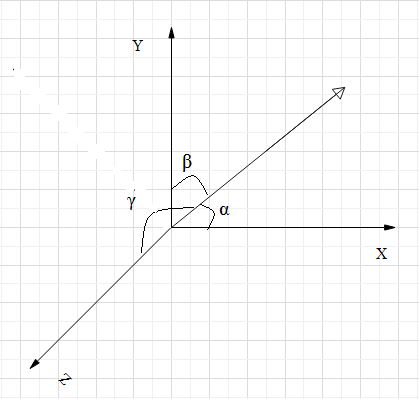
The angle made from the x-axis is called the alpha ($\alpha$)
The angle made from the y-axis is called the beta ($\beta$)
The angle made from the z-axis is called the gamma ($\gamma$)
The relation between these angles made from the x-axis, y-axis and the z-axis is given as follows.
${{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =1$
The value of the cos angle varies between,

& -1<\cos \theta <1 \\\ & \Rightarrow 0<\cos \theta <1 \\\ \end{aligned}$$ We will use hit and trial methods to solve this problem. Consider the first option, $$A.\,45{}^\circ ,\,60{}^\circ $$ Substitute these angle values in the above equation. So, we get, $$\begin{aligned} & {{\cos }^{2}}45{}^\circ +{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}\gamma =1 \\\ & \Rightarrow \dfrac{1}{2}+\dfrac{1}{4}+{{\cos }^{2}}\gamma =1 \\\ & \Rightarrow {{\cos }^{2}}\gamma =\dfrac{1}{4} \\\ \end{aligned}$$ So, this value of the angles lies between the limits of the cos function. Hence, this set of a and b is possible. Consider the second option, $$B.\,30{}^\circ ,\,60{}^\circ $$ Substitute these angle values in the above equation. So, we get, $$\begin{aligned} & {{\cos }^{2}}30{}^\circ +{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}\gamma =1 \\\ & \Rightarrow \dfrac{3}{4}+\dfrac{1}{4}+{{\cos }^{2}}\gamma =1 \\\ & \Rightarrow {{\cos }^{2}}\gamma =0 \\\ \end{aligned}$$ So, this value of the angles lies between the limits of the cos function. Hence, this set of a and b is possible. Consider the third option, $$C.\,60{}^\circ ,\,60{}^\circ $$ Substitute these angle values in the above equation. So, we get, $$\begin{aligned} & {{\cos }^{2}}60{}^\circ +{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}\gamma =1 \\\ & \Rightarrow \dfrac{1}{4}+\dfrac{1}{4}+{{\cos }^{2}}\gamma =1 \\\ & \Rightarrow {{\cos }^{2}}\gamma =\dfrac{1}{2} \\\ \end{aligned}$$ So, this value of the angles lies between the limits of the cos function. Hence, this set of a and b is possible. Consider the fourth option, $$D.\,30{}^\circ ,\,45{}^\circ $$ Substitute these angle values in the above equation. So, we get, $$\begin{aligned} & {{\cos }^{2}}30{}^\circ +{{\cos }^{2}}45{}^\circ +{{\cos }^{2}}\gamma =1 \\\ & \Rightarrow \dfrac{3}{4}+\dfrac{1}{2}+{{\cos }^{2}}\gamma =1 \\\ & \Rightarrow {{\cos }^{2}}\gamma =-\dfrac{1}{4} \\\ \end{aligned}$$ So, this value of the angles does not lie between the limits of the cos function. Hence, this set of a and b is not possible. As the set of a and b, that is $$30{}^\circ ,\,45{}^\circ $$ is not possible, thus, the option (D) is correct. **Note:** The things to be on your finger-tips for further information on solving these types of problems are: A trick to solve this type of problem is, they have given that the angles are made from the positive x-axis and positive y-axis. The angular difference between these two axes is 90 degrees, thus, the set whose angles sums less than 90 degrees do not belong to the set.