Question

(a) An iron ring of relative permeability $\mu _r$, has windings of insulated copper wire of $n$ turns per metre. When the current in the windings is $I$, find the expression for the magnetic field in the ring.
(b) The susceptibility of a magnetic material is 0.9853. Identify the type of magnetic material. Draw the modification of the field pattern or keeping a piece of this material in a uniform magnetic field

Answer 1

(a) The definition of Ampere’s law would be implanted in the question to find the value of the magnetic field.
(b) The direction of magnetic field lines is from north to mouth the magnetic susceptibility of the material is positive and lies between 0 and 1. So, that is the property of paramagnetic material, when c paramagnetic substance is placed in a uniform magnetic field the unpaired electron aligns itself with the external field.

Complete step by step answer:
(a) Ampere’s law states that the line integral of magnetic field B around any closed circuit is equal to the total current passing through it in a closed circuit. Mathematically, it can be expressed as
$\int {\overrightarrow B \cdot \overrightarrow {dL} } = {\mu _0}\,{\mu _r}\,{I_e}$…… (i)

If B is a constant and directed along the tangent to every point on the perimeter L of a closed curve and Ie is the enclosed current, ${\mu _0}$ is the permeability of free air and ${\mu _r}$ is the relative permeability.

The magnetic field inside the ring is,
$\int {\overrightarrow B \cdot \overrightarrow {dL} } = B\int {\overrightarrow {dL} }$

$\int {\overrightarrow B \cdot \overrightarrow {dL} } = B \cdot \left( {2\pi r} \right)$…… (ii)

where $\int {\overrightarrow {dL} = 2\pi r}$ is the circumference of the ring and r is the radius.

${I_e} = 2\pi rnI$
Where n = number of turns per meter

Therefore, on equating equation (i) and (ii), to find the magnetic field B.

$${\mu _0}\,{\mu _r}\,{I_e} = B \cdot 2\pi r \\\ {\mu _0}\,{\mu _r}\left({2\pi r n I}\right) = B \cdot 2\pi r \\\ B = {\mu _0}\,\mu \,n\,I \\\$$

There the magnetic field is $B = {\mu _0}\,\mu \,n\,I$.

(b) When a paramagnetic material is placed in a uniform magnetic field, then the magnetic field lines are shown as:

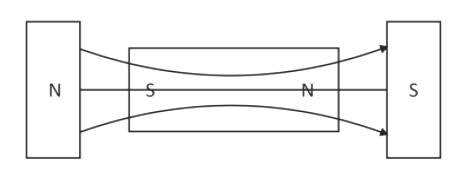
Note:
(a) The line integral of magnetic field B around any closed circuit is equal to times the total current passing through the closed loop
(b) The magnetic susceptibility of paramagnetic material is between 0 and 1.