Question

(a) An EM wave is travelling in a medium with a velocity $v=v\widehat{i}$. Draw a sketch showing the propagation of the EM wave, indicating the direction of the oscillating electric and magnetic fields.
(b) How are the magnitudes of the electric and magnetic fields related to velocity of the EM wave?

Answer 1

Electromagnetic waves are those waves which have changing electric and magnetic fields while transporting energy and momentum through space. They require no medium and can travel through vacuum.

Complete step-by-step answer:
EM waves are known as the solutions of Maxwell’s equations. Sinusoidal plane waves are one of the types of electromagnetic waves. Not all EM waves are considered to be sinusoidal, but all EM waves can be viewed as linear superposition of sinusoidal plane waves travelling in particular directions.
A plane wave travelling in x-direction will be of the form,
${{E}_{(x,t)}}={{E}_{\max }}\cos (kx-\omega t+\phi )$
${{B}_{(x,t)}}={{B}_{\max }}\cos (kx-\omega t+\phi )$
Where, ‘E’ and ‘B’ are the electric and magnetic fields of the EM waves.
For an EM wave, electric and magnetic fields are always perpendicular to each other and also perpendicular to the direction of propagation. $\overrightarrow{E}\times \overrightarrow{B}$ gives the direction of propagation of the wave.
(a) The given velocity is $v=v\widehat{i}$. With electric field ‘E’ along x-axis and the magnetic field ‘B’ along z-axis, the propagation of EM wave can be illustrated as:

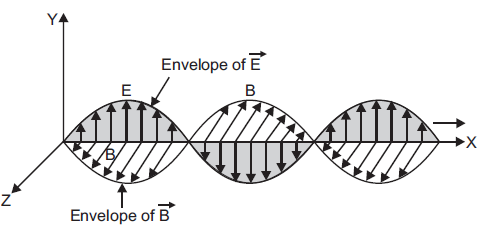
Let $\widehat{i}$ denote the x-direction, $\widehat{j}$ the y-direction $\widehat{k}$ and the z-direction.
The direction of oscillating field can be written as $\widehat{\hat{i}}=\widehat{j}\times \widehat{k}$
(b) As electromagnetic waves are transverse and they propagate at a speed ‘c’. The relation between the electric and magnetic field of an EM wave is given by the ratio of magnitude of electric field to the magnitude of magnetic field.
$c=\dfrac{{{E}_{0}}}{{{B}_{0}}}$

Note: Electromagnetic waves are transverse waves. The speed of any EM wave in free space is equal to the speed of light i.e., $c=3\times {{10}^{8}}m{{s}^{-1}}$. Electromagnetic waves may have any range of wavelength ‘λ’ and frequency ‘f’ as their relation is given as $\lambda f=c$.