Question

If $A = \begin{bmatrix} x & 1 \\ 1 & 0 \end{bmatrix}$ and $A^2 = I$, then $A^{-1} =$

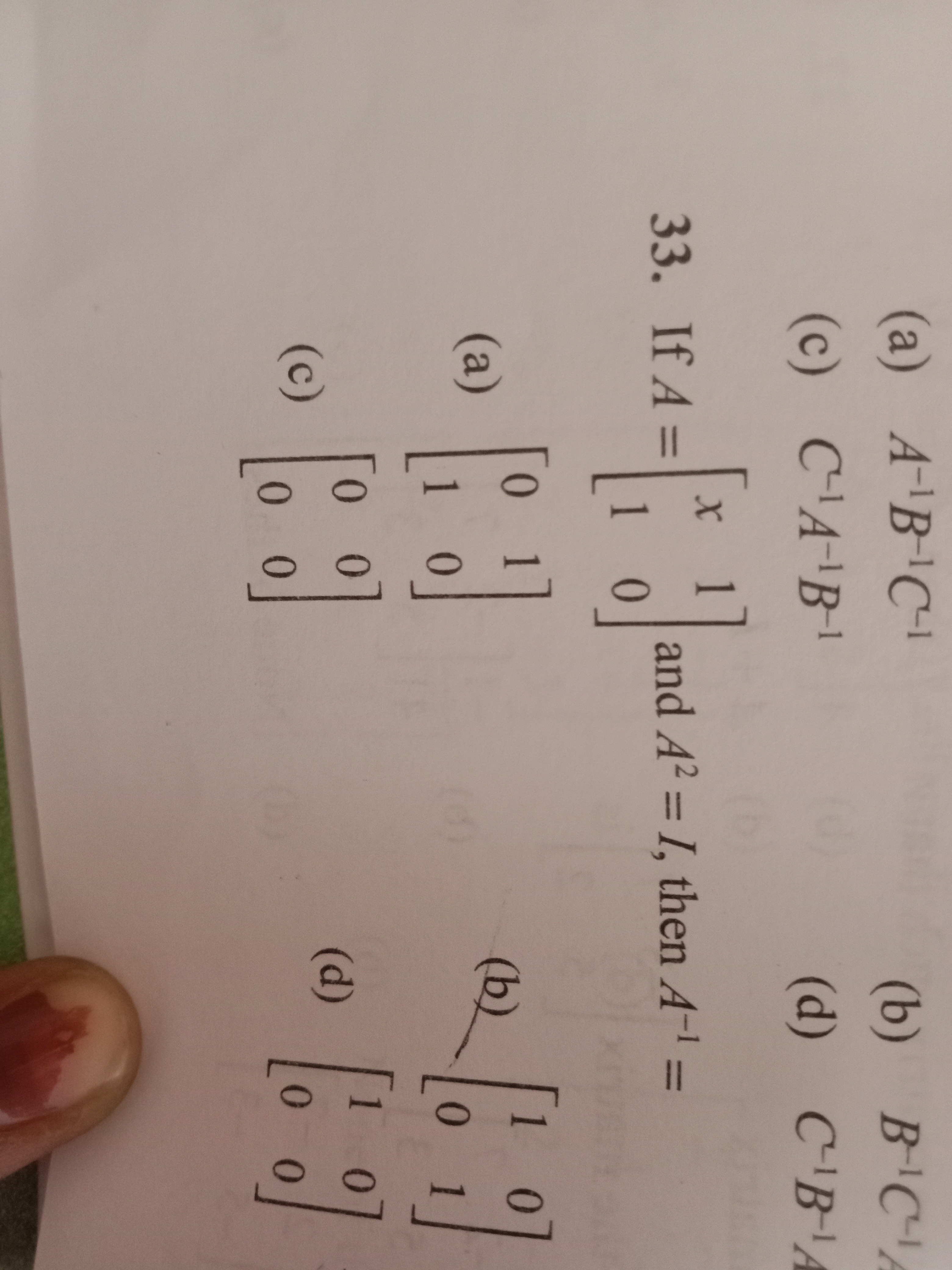
• A. $\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$
• B. $\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$
• C. $\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$
• D. $\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}$

Answer 1

Answer: (A)

$\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$

Answer 2

Given $A = \begin{bmatrix} x & 1 \\ 1 & 0 \end{bmatrix}$ and $A^2 = I$, we first compute $A^2$:

$A^2 = \begin{bmatrix} x & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} x & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} x^2+1 & x \\ x & 1 \end{bmatrix}$.

Since $A^2 = I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$, we equate the elements:

• $x^2 + 1 = 1 \Rightarrow x^2 = 0 \Rightarrow x = 0$
• $x = 0$
• $1 = 1$

Thus, $A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$.

Since $A^2 = I$, $A$ is its own inverse. Therefore, $A^{-1} = A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$.