Question

(a) A point object O is kept in a medium of refractive index n in front of a convex spherical surface of curvature R which separates the second medium of refractive index n2 from the first one as shown in the figure. Draw the ray diagram showing the image formation and deduce the relationship between the object distance and the image distance in terms of n1, n2, and R.

(b) When the image formed above acts as a virtual object for a concave spherical surface separating the medium n2 and n1 (n2 > n1) draw this ray diagram and write a similar relation. Hence obtain the expression for lens maker’s formula

Answer 1

Recall the relationship between the object distance and the image distance in terms of the refractive of the medium in which the object is placed and the refractive index of the lens and the radius of curvature. Recall the lens maker formula and draw the proper ray diagram,

Complete step by step solution:
(a) The ray diagram showing the formation of image is given below:

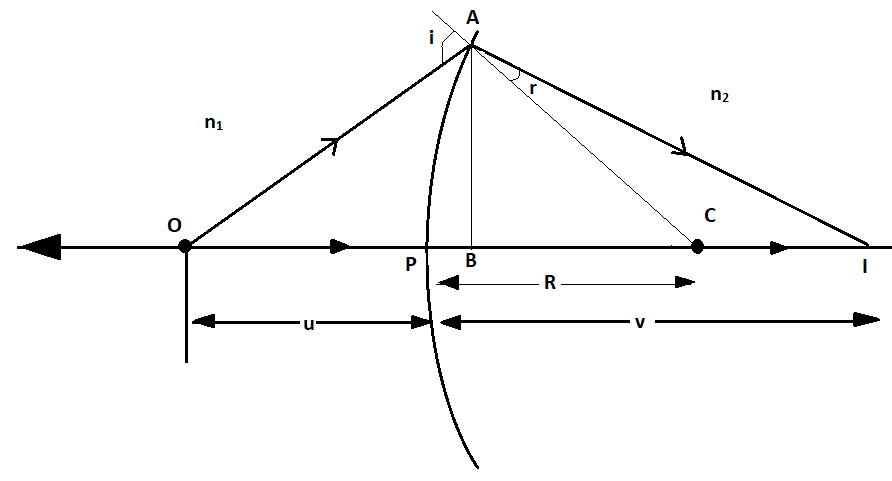
The object O is placed in the medium having refractive index ${n_1}$ and the ray is incident from that medium to another medium of refractive index ${n_2}$.
Here, AB is taken as the perpendicular to the principal axis.
Here, all the angles are very very small,
So,
$\tan \angle AOB = \dfrac{{AB}}{{OB}}$
As the angle is very small, this becomes
$\Rightarrow \dfrac{{AB}}{{OB}} \cong \angle AOB$
Now, $\tan \angle ACB = \dfrac{{AB}}{{BC}}$
As the angle is very small, this becomes
$\Rightarrow \dfrac{{AB}}{{BC}} \cong \angle ACB$
Again, $\tan \angle AIB = \dfrac{{AB}}{{BI}}$
As the angle is very small, this becomes
$\Rightarrow \dfrac{{AB}}{{BI}} \cong \angle AIB$
Now in $\vartriangle AOC$
Here, it is the exterior angle.
Therefore, $i = \angle AOB + \angle ACB$ ……………..(i)
On putting the values from above equations, we get
$\Rightarrow i = \dfrac{{AB}}{{OB}} + \dfrac{{AB}}{{BC}}$
Similarly, in $\vartriangle ACI$
$r = \angle ABC - \angle AIB$ ………….(ii)
On putting values from above equations we get,
$\Rightarrow r = \dfrac{{AB}}{{BC}} + \dfrac{{AB}}{{BI}}$
Now using snell’s law, we have
${n_1}\sin i = {n_2}\sin r$
For very small angle we have,
$\Rightarrow {n_1}i = {n_2}r$
Now on putting values from equation (i) and (ii), we have
$\Rightarrow {n_1}\left( {\dfrac{{AB}}{{OB}} + \dfrac{{AB}}{{BC}}} \right) = {n_2}\left( {\dfrac{{AB}}{{BC}} + \dfrac{{AB}}{{BI}}} \right)$
On further solving, we get
$\Rightarrow \dfrac{{{n_1}}}{{OB}} + \dfrac{{{n_2}}}{{BI}} = \dfrac{{{n_2} - {n_1}}}{{BC}}$
Now, from the ray diagram, we have
$OB = - u$
$BI = + v$
$BC = + R$
On putting these values on the above equation we get,
$\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R}$ ……….(iii)
This is the answer for the first part.

(b) The ray diagram is formed as

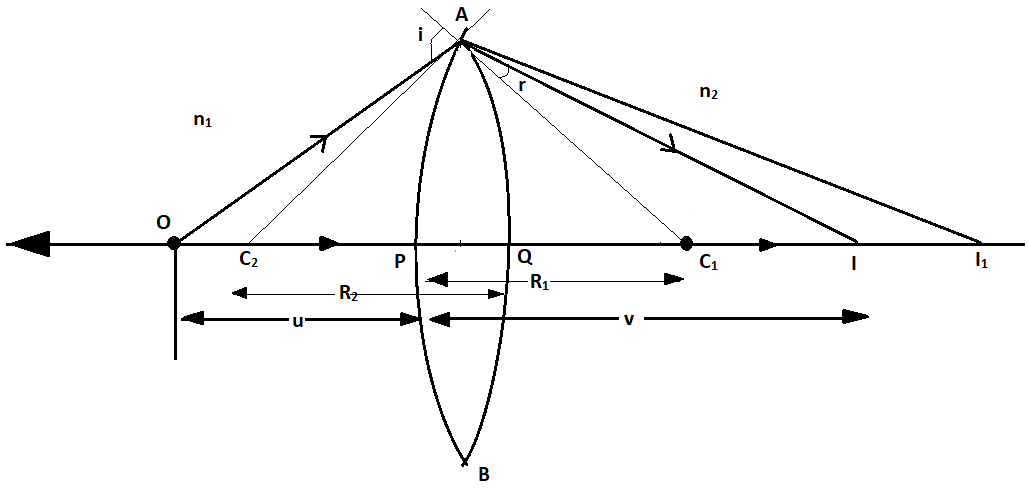
The image formed in the above part is virtual image, so it acts as a virtual object for a concave spherical surface,
Refraction from both surfaces,
$\dfrac{{{n_1}}}{v} - \dfrac{{{n_1}}}{u} = ({n_2} - {n_1})\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Dividing whole equation by ${n_1}$, we have
$\Rightarrow \dfrac{1}{v} - \dfrac{1}{u} = \left( {\dfrac{{{n_2}}}{{{n_1}}} - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
On putting, $u = \infty ,v = f$, we get
$\Rightarrow \dfrac{1}{f} = \left( {\dfrac{{{n_2}}}{{{n_1}}} - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Hence we obtained the lens maker formula.

Note: Lens maker’s formula is the relation between the focal length of a lens to the refractive index of its material and the radii of curvature of its two surfaces. It is used by lens manufacturers to make the lenses of particular power from the glass of a given refractive index.