Question

A $9V$ battery with an internal resistance of $0.5\Omega$ is connected across an infinite network as shown in the figure. All ammeters ${A_1},{A_2},{A_3}$ and voltmeter $V$ are ideal. Choose the correct statement.

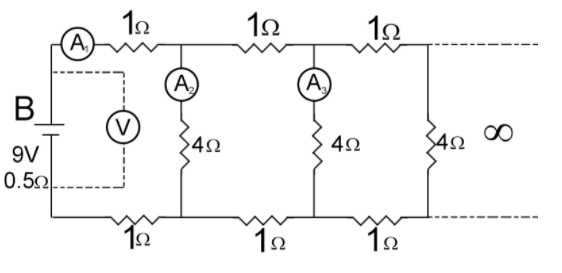
A.Reading of ${A_1}$ is $2A$ .
B.Reading of $V$ is $7V$ .
C.Reading of $V$ is $9V$ .
D.Reading of ${A_1}$ is $18A$ .

Answer 1

You can start by defining ohm’s law, voltmeter and ammeter. Then draw a new diagram of the circuit and in it replace the infinite resistors with a resistor $y$ which will be the effective resistance of the circuit. Then given that the fact some new resistors will not change the effective resistance of the circuit significantly, you can use $1 + \dfrac{{4y}}{{4 + y}} + 1 = y$ to find the value of $y$ . Then use the equation $I = \dfrac{E}{{r + R}}$ to find the value of ${A_1}$ . Then use the equation $V = E - IR$ to find the value of $V$ .

Complete answer:
Ohm’s law – This law defines the relationship between current and voltage. According to ohm’s law, the current flowing through a conductor is directly proportional to the voltage difference across the ends of the conductor.
$I \propto V$
$I = \dfrac{V}{R}$
Here $I =$ current, $V =$ Voltage, and $R =$ resistance
Voltmeter – It is electrical equipment that is used to measure the potential difference between two points on an electrical circuit.
Ammeter - It is a piece of electrical equipment that is used to measure the circuit flowing two points on an electrical circuit or through a whole circuit.
In this system, we have an infinite network of resistors. An infinite network means that the addition of a few more resistors will not affect the effective resistance of the system significantly.
Let’s arrange the given circuit in the following form.

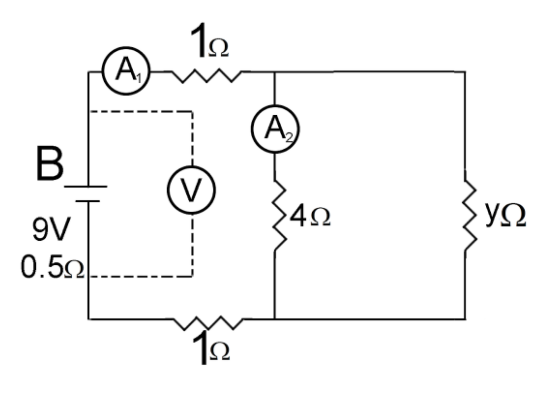
Here $y$ is the effective resistance of the infinite system of the resistor.
The resistance of parallel resistors $y$ and $4\Omega$ are
$\dfrac{{4y}}{{4 + y}}$
So the total effective resistance of the circuit is equal to
$1 + \dfrac{{4y}}{{4 + y}} + 1 = y$
$4y + 2(4 + y) = y(4 + y)$
$6y + 8 = 4y + {y^2}$
${y^2} - 2y - 8 = 0$
Solving this quadratic equation
$y = \dfrac{{2 \pm \sqrt {4 + 32} }}{2}$
$y = \dfrac{8}{2}$
$y = 4\Omega$
For the ammeter reading that measures the total current in the circuit
$I =$ Current through ${A_1} = \dfrac{E}{{r + R}} = \dfrac{9}{{0.5 + 4}} = 2A$
Here, $r =$ The internal resistance of the battery and $R =$ effective resistance of the given circuit
For the voltmeter reading that is connected across the battery
$V = E - IR = 9 - 2 \times 0.5$
$V = 8V$

Hence, option A is the correct choice.

Note:
In the solution above we said that $1 + \dfrac{{4y}}{{4 + y}} + 1 = y$ is equal to the effective resistance of the circuit. This can be a bit confusing, but remember $y$ is the result of a combination of infinite resistors, so adding a few more resistors to the circuit will not make the effective resistance significantly different. In reality, the effective resistance will change but we usually ignore it for such problems.