Solveeit Logo
Login

Question

Question: A 9V battery is connected to a bulb whose resistance is \(3000\;\Omega\). How many electrons leave t...

A 9V battery is connected to a bulb whose resistance is 3000  Ω3000\;\Omega. How many electrons leave the battery per minute?

Explanation

Solution

We know that a battery establishes a potential difference across the ends of the circuit enabling current to flow through it. In such a case, first determine the current across the circuit supplied by the battery. Then, we know that the current is nothing but charge flowing through the circuit in unit time. To this end, determine the charge through the circuit, and by considering the charge possessed by a single electron, deduce the number of electrons leaving the battery in one minute. Pay caution to the unit of time for all calculations.
Formula Used:
Current I=VRI = \dfrac{V}{R}
Charge Q=I×tQ = I \times t

Complete answer:
We are given that V=9  VV =9\;V and R=3000  ΩR = 3000\;\Omega.

Therefore, the current flowing in the bulb due to the battery can be given by:
I=VR=93000=3×10−3  AI = \dfrac{V}{R} = \dfrac{9}{3000} = 3 \times 10^{-3}\;A
Now, we know that current is equivalent to the charge flowing out the battery in unit time, i.e.,
I=QtI = \dfrac{Q}{t}
Therefore, the charge flowing out the battery can be given as:
Q=I×tQ = I \times t
Taking t=1  min=60  st = 1\;min = 60\;s and I=3×10−3  AI = 3 \times 10^{-3}\;A the above equation becomes:
Q=3×10−3×60=180×10−3  CQ = 3 \times 10^{-3} \times 60 = 180 \times 10^{-3}\;C
Now, we know that a single electron carries a charge of 1.6×10−19  C1.6 \times 10^{-19}\;C
Therefore, the number of electrons carrying a charge of Q=180×10−3  CQ= 180 \times 10^{-3}\;C will be:
n=180×10−31.6×10−19=112.5×10−3+19=112.5×1016≈113×1016n = \dfrac{180 \times 10^{-3}}{1.6 \times 10^{-19}} = 112.5 \times 10^{-3+19} = 112.5 \times 10^{16} \approx 113 \times 10^{16}
Thus, about 113×1016113 \times 10^{16} electrons leave the battery per minute.

Note:
It is important to understand the distinction between electron flow and conventional current flow. Electrons flow from the negative terminal of the battery to the positive terminal and constitute the electron current whereas positive charges move in an opposite direction and constitute the conventional current.

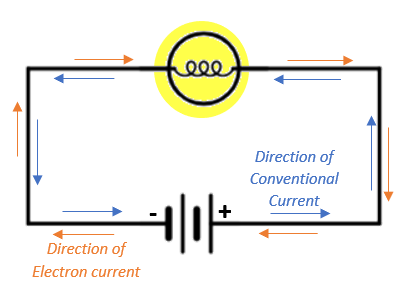
Keep in mind that the electric current in a circuit arises only from the flow of electrons and not from the flow of positively charged particles. Thus, conventional current is defined as if the movement of positive charge carriers constitute electric current flow when it is in fact not the case.