Question
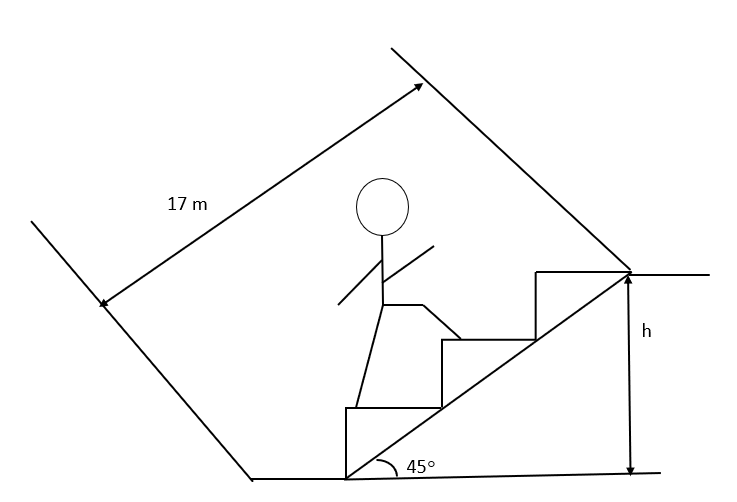
Question: A 90-kg man runs up an escalator while it is not in operation in 10s as shown in figurer. What is th...
A 90-kg man runs up an escalator while it is not in operation in 10s as shown in figurer. What is the average power developed by man. Suppose next that the escalator is running so that the escalator steps move at a speed of 0.6m/s. what is then the power developed by the man as seen by the ground reference if he moves at the same speed relative to the escalator steps as he did when the escalator is not in operation?
Solution
In this question, firstly we have to calculate the work required by the man in climbing the escalator. Then, Power and velocity are required to calculate. After that, calculate relative time and find power with the help of this time.
Formula used:
Here, two formulas are used, one is of power, P=tW.
Where,Wis work done and tis the time required for work to be done.
Another is of Velocity,V=td. Where d is the distance that the object has travelled and is the time in which 'd' distance is travelled by the object.
Complete step-by-step solution:
Work done by the man in climbing the escalator is :-
W=90\times 9.8\times 17sin{{45}^{o}}$$$$W=mgh
W=90×9.8×17sin45∘
W=10611J
With the escalator stationary, man takes 10s to climb up. Therefore, average power is :-
P=tW
P=1010611
P=1061.1W
Speed of the man when escalator is stationary is :-
Velocity,V=td
V=1017
V=1.7m/s
In the second case, the speed of the man relative to the moving escalator is also 1.7m/s.
His speed relative to the ground is 0.6+1.7 = 2.3 m/s.
Accordingly, the time taken by the man in climbing is :-
t=2.317
t=7.4s
The average power developed by the man as seen from the ground reference is :-
P=tW
P=7.410611
P=1434W
Note: Don't get confused while solving equations. Also, to get rid of that, always prefer solving equations in a stepwise manner. Attention, we are solving equations with the help of results obtained from preceding equations. So, do it in that manner.
