Question

A $9 - volt$ battery is connected to four resistors to form a simple circuit as shown below. What would be the electric potential at point $B$ with respect to point $C$ in the above circuit?

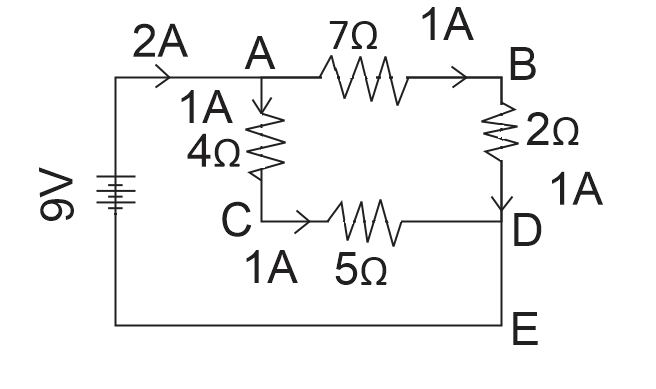
A. $+ 7V$
B. $+ 3V$
C. $0V$
D. $- 3V$

Answer 1

Simplify the circuit to calculate equivalent resistance along AD.
From this, calculate current through each arm of the circuit. Then use it to solve the question.

Formula used:
For seems:
${R_{eq}} = {R_1} + {R_2}$
$\dfrac{1}{{{R_q}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
$v = 1R$

Complete step by step answer:

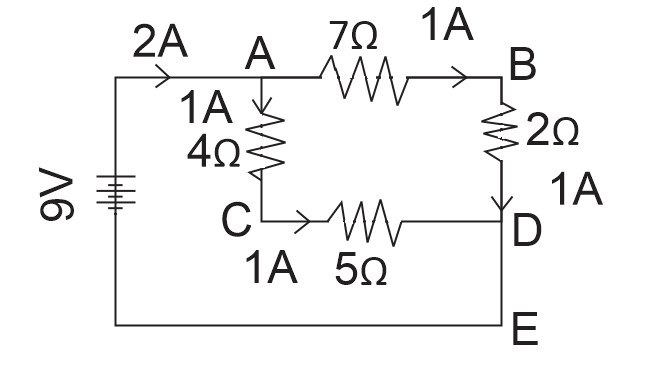
We can clearly observe that the resistances, $7\Omega$ and $2\Omega$, and also, $4\Omega$ and $5\Omega$
Between points A and D are converted in since to each other.
Since, for series resistance
${K_{eq}} = {R_1} + {R_2}$
We get
${R_1} = 7 + 2$and
${R_2} = 4 + 5$
Then the circuit will simplify to

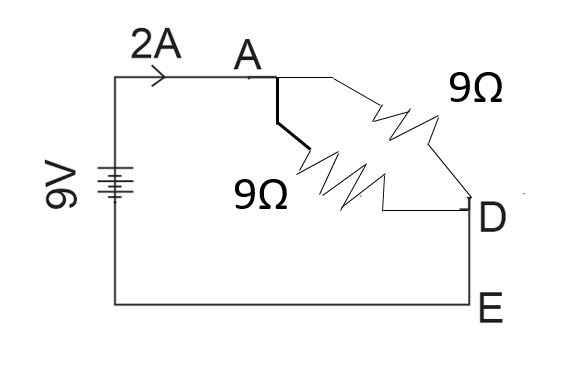
Now, the resistances between A and D are commented is formula.
We know, for parallel commotion.
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
$\dfrac{1}{{{R_{eq}}}} = - \dfrac{1}{9} + \dfrac{1}{9}$
$= \dfrac{2}{9}$ (By taking LCM and adding)
By taking reciprocal
We get,
${R_{eq}} = \dfrac{9}{2}$
$\Rightarrow {R_{eq}} = 4.5\Omega$
Now, by ohm’s law
We know that
$v = 1R$
Where, $v$is partial
$I$is correct
$R$is resistance
By re-arranged the equation
We get,
By substituting the values in it,
We get,
$I = \dfrac{9}{{4.5}}$ ($\because v = 9v,R = 4.5\Omega$)
$\Rightarrow I = 2A$
Therefore, the total current flowing through the circuit is $2A.$
Now, if we observe the last circuit diagram,
We can see that the resistance between both the arms of AD is the same.
Hence, equal current most parts through them
Therefore, we can say that
1A current is passing through ABC.
And 1A current is passing.
Through ACD
Now, for the simplicity of calculation.
Let us imagine that the potential of the negative terminal battery is zero.
Then the potential at the positive terminal will be$9v$.
Therefore, we can writ potential at be
${v_B} = 9 - (7 \times 1)(\because EMF = 9,R = 7,I = 1)$
$\Rightarrow {v_B} = 2v$
Simplify, potential at $c$
$i.e{V_c} = 9 - (4 \times 1)$
$\Rightarrow {V_c} = 5V$
Therefore, potential at point BV with respect to potential at point C is
${V_C} = {V_C} - {V_B}$
$\Rightarrow {V_{BCC}} = 5 - 2$
$\Rightarrow {V_{BC}} = 3v$

So, the correct answer is “Option B”.

Note:
For this question you need to be able to figure out which resistance are connected in series and which are parallel.
Every given information is important like in this question knowing that the resistance between A and D are equal helped us to understand that equal current will flow through them.