Question

A $70\;kg\;$ man stands in contact against the inner wall of a hollow cylindrical drum of radius $3\;m\;$rotating about its vertical axis with $200\;rev/min$. The coefficient of friction between the wall and his clothing is $0.15$. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?

Answer 1

We know that the velocity of a particle has two parts: magnitude and direction. When an object is moving in a circular path the magnitude of the velocity of the particle remains the same but its direction part will be constantly changing. Change in any part of the velocity will lead to acceleration. In the case of circular motion, it is called angular acceleration.

Complete step by step solution:

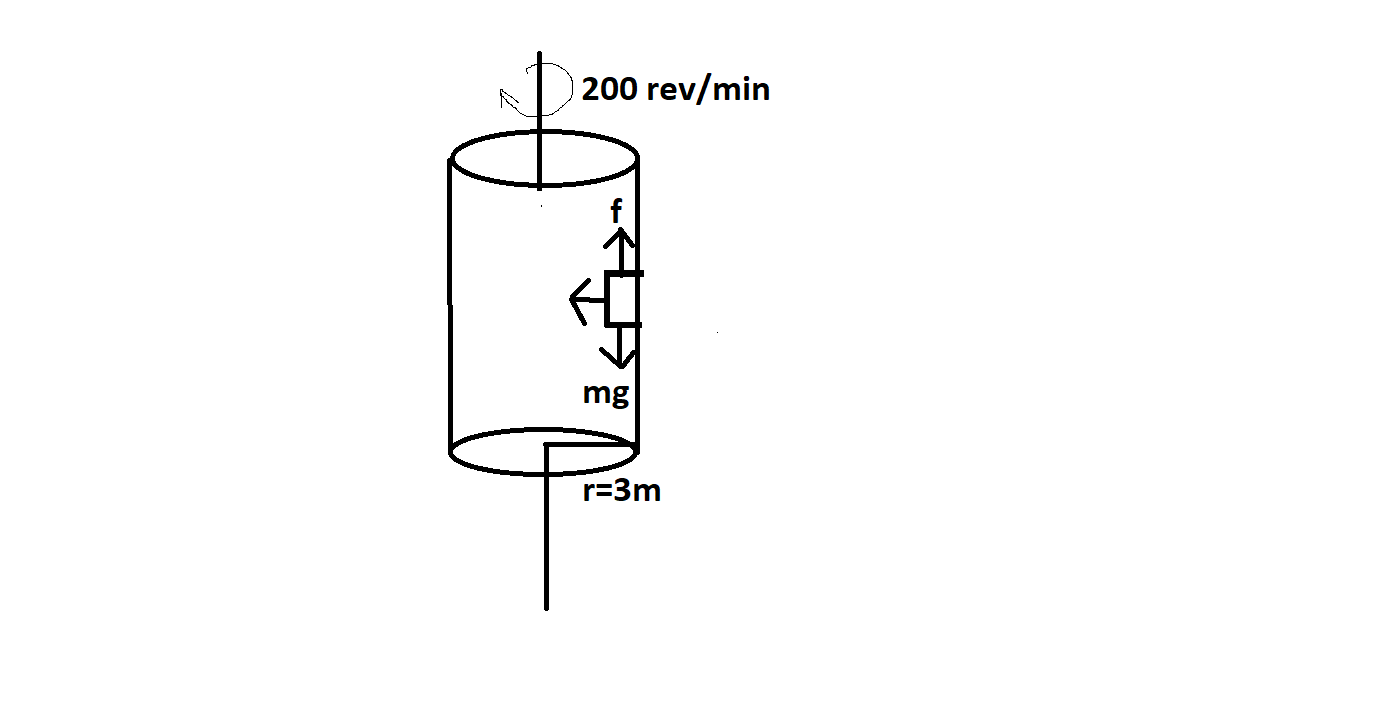
Given that the mass of man $m$=$70\;kg\;$
The radius of the drum $r = 3m$
Coefficient of friction $\mu = 0.15$
Frequency of the rotation $\omega = 200rev/\min$
Converting this $rev/\sec$,
$\omega = \dfrac{{200}}{{60}}rev/\sec$
$\omega = \dfrac{{10}}{3}rev/\sec$
Any object which travels in circular motion needs centripetal force. The centripetal acceleration is directed normally to the velocity and passes through the center of the circular path.
Given that the cylinder is rotating about the axis of rotation. So the velocity changes its direction constantly which makes it accelerate. Because the velocity is changing in every location and the object is moving in a circular motion, there should be a force in the radial direction. This radial force also acts on the man and this radial force tries to make the person move towards the center of the cylinder. Since there is a radial force there is an opposite force acting upon the person.
Now, this centripetal force that is needed is provided by the normal force ${F_N}$. Therefore this normal force is equal to the centripetal force.
${F_N} = m\omega {r^2}$
The normal force is the opposite force of gravitational force. When the drum revolves around the man will stick on the wall of the drum. Hence the weight of the man acting downward is balanced by the frictional force ${F_k}$ acting upward.
Hence the man will not fall until $mg < \mu {F_N}$
$\Rightarrow mg < \mu m\omega {r^2}$
$\Rightarrow g < \mu \omega {r^2}$
Therefore the minimum needed angular speed is given as,
${\omega _{\min }}^2 = \dfrac{g}{{\mu \times r}}$
Here $g$ is the acceleration due to gravity ($g = 10m/{s^2}$)
$\mu$ is the kinetic friction ($\mu = 0.15$)
$r$ is the radius of the drum $r = 3m$
Substituting all the values,
{\omega _{\min }}^2 = \dfrac{{10}}{{0.15 \times 3}}$$$$ = 22.2
$\omega = 4.7rad/s$
Therefore the minimum rotational speed of the cylinder to prevent the man from falling is $4.7rad/s$

Note:
We have in the above problem that only the direction of the velocity changes and not the magnitude. If suppose both the magnitude and the direction changes it is called Tangential acceleration. The acceleration that alters the magnitude of the velocity is called tangential motion.