Question
Question: A(6,1), B(8,2) and C(9,4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, fi...
A(6,1), B(8,2) and C(9,4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of △ADE.
A. 6 sq. units
B. 23 sq. units
C. 43 sq. units
D. 12 sq. units
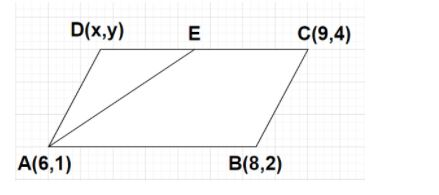
Solution
Here, we will proceed by finding out the coordinates of the vertex D of the parallelogram ABCD using distance formula i.e., D=(d−b)2+(c−a)2 and property of the parallelogram i.e., the pair of any two opposite sides are always equal in length.
Complete step-by-step answer:
Let us consider a parallelogram ABCD having vertices as A(6,1), B(8,2), C(9,4) and D(x,y). Point E is the midpoint of side DC as shown in the figure.
As we know that according to distance formula, the distance between any two points (a,b) and (c,d) is given by
D=(d−b)2+(c−a)2 →(1)
Using equation (1), the distance between the points A(6,1) and B(8,2) is given by
AB = (2−1)2+(8−6)2=12+22=1+4=5 units
Using equation (1), the distance between the points B(8,2) and C(9,4) is given by
BC = (4−2)2+(9−8)2=22+12=4+1=5 units
Using equation (1), the distance between the points C(9,4) and D(x,y) is given by
CD = (y−4)2+(x−9)2=(y2+42−8y)+(x2+92−18x)
⇒CD=y2+16−8y+x2+81−18x=y2−8y+x2−18x+97units
Using equation (1), the distance between the points D(x,y) and A(6,1) is given by
⇒DA = (1−y)2+(6−x)2=(12+y2−2y)+(62+x2−12x)
⇒DA = 1+y2−2y+36+x2−12x=y2−2y+x2−12x+37 units
According to the property of parallelogram, the pair of any two opposite sides are always equal in length
i.e., For any parallelogram ABCD, AB = CD and BC = DA
By substituting the values of AB, BC, CD and DA obtained in the above two equations, we get
⇒5=y2−8y+x2−18x+97 and ⇒5=y2−2y+x2−12x+37
Squaring on both sides of the above two equations, we get
⇒5=y2−8y+x2−18x+97 ⇒y2−8y+x2−18x+92=0 →(2) and
⇒5=y2−2y+x2−12x+37 ⇒y2−2y+x2−12x+32=0 →(3)
By subtracting equation (2) from equation (3), we get
By substituting the value of x from equation (4) in equation (2), we get
⇒y2−8y+(10−y )2−18(10−y )+92=0 ⇒y2−8y+(100+y2−20y)−(180−18y )+92=0 ⇒y2−8y+100+y2−20y−180+18y+92=0 ⇒2y2−10y+12=0 ⇒2(y2−5y+6)=0 ⇒y2−5y+6=0The above quadratic equation in y can be solved by splitting the middle term method.
⇒y2−2y−3y+6=0 ⇒y(y−2)−3(y−2)=0 ⇒(y−3)(y−2)=0Either
y - 3 = 0 \\\ \Rightarrow y = 3 \\\ $$ ory - 2 = 0 \\
\Rightarrow y = 2 \\
