Solveeit Logo
Login

Question

Question: A \(60pF\) capacitor is fully charged by a \(20V\) supply. It is then disconnected from the supply a...

A 60pF60pF capacitor is fully charged by a 20V20V supply. It is then disconnected from the supply and is connected to another uncharged 60pF60pF capacitor in parallel. The electrostatic energy that is lost in this process by the time the charge is redistributed between them is (in nJ) ______.

Explanation

Solution

We will find initial charge on initial capacitor of 60pF60pF and total energy of circuit. Then after adding a second capacitor, we will do voltage balance in the circuit. From there we will find the final charge in both capacitors. Then we will find the final energy of the circuit. The difference between final and initial energies will be the energy loss in the process.

Complete step-by-step solution: Let initial charge on capacitor be Q0{Q_0}
Then, Q0=C1V{Q_0} = {C_1}V
Where C1=60pF{C_1} = 60pF and V=20VV = 20V

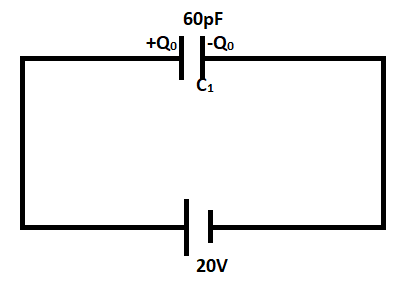
Therefore, Q0=60×10−10×20{Q_0} = 60 \times {10^{ - 10}} \times 20
So we get,
Q0=120×10−10C{Q_0} = 120 \times {10^{ - 10}}C
Therefore, Q0=1200pC{Q_0} = 1200pC
Initial energy Ui{U_i} is given by 12C1V2\dfrac{1}{2}{C_1}{V^2}
On putting values, we get,
Ui=12×60×10−10×(20)2{U_i} = \dfrac{1}{2} \times 60 \times {10^{ - 10}} \times {(20)^2}
So we get,
Ui=120×10−10J{U_i} = 120 \times {10^{ - 10}}J
When battery is disconnected and new capacitor is added, then,
Let final charge on first capacitor be Qf{Q_f} and charge on second capacitor be qq

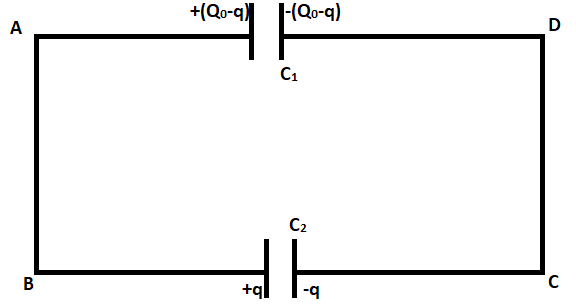
Therefore, Qf=Q0−q{Q_f} = {Q_0} - q

Doing force balance on above circuit, we get the equation,
VB−qC2+Q0−qC1=VB{V_B} - \dfrac{q}{{{C_2}}} + \dfrac{{{Q_0} - q}}{{{C_1}}} = {V_B} ,
On simplifying we get,
Q0−qC1=qC2\dfrac{{{Q_0} - q}}{{{C_1}}} = \dfrac{q}{{{C_2}}} ,
Putting values we get,
1200−q60=q60\dfrac{{1200 - q}}{{60}} = \dfrac{q}{{60}} ,
On simplifying we get,
1200=2q1200 = 2q ,
On further simplification, we get,
q=600pCq = 600pC
So, Qf=Q0−q{Q_f} = {Q_0} - q
So we get,
Qf=1200−600=600{Q_f} = 1200 - 600 = 600
Final energy Uf{U_f} is the sum of energies in both capacitors so,
Uf=Qf22×C1+q22×C2{U_f} = \dfrac{{{Q_f}^2}}{{2 \times {C_1}}} + \dfrac{{{q^2}}}{{2 \times {C_2}}}
On putting values we get,
Uf=(600)22×60+(600)22×60{U_f} = \dfrac{{{{\left( {600} \right)}^2}}}{{2 \times 60}} + \dfrac{{{{\left( {600} \right)}^2}}}{{2 \times 60}}
On solving we get,
Uf=60×10−10J{U_f} = 60 \times {10^{ - 10}}J
Energy lost is Ui−Uf{U_i} - {U_f}
So, energy loss = 120×10−10J−60×10−10J{\text{energy loss = 120}} \times {\text{1}}{{\text{0}}^{ - 10}}J - 60 \times {10^{ - 10}}J
On solving, energy loss = 12×10−9J−6×10−9J{\text{energy loss = 12}} \times {\text{1}}{{\text{0}}^{ - 9}}J - 6 \times {10^{ - 9}}J
On solving we get,
energy loss = 6×10−9J = 6nJ{\text{energy loss = }}6 \times {10^{ - 9}}J{\text{ = 6nJ}}
So, answer is 66

Note:- We subtracted final energy from initial energy in solution because initial energy will be greater than final energy. Energy loss in the process is due to heat generated while connecting the initial capacitor with the second capacitor. That’s why energy loss is in the form of heat.