Question

A $60\,{\text{kg}}$ body is pushed with just enough to start it moving across a floor and the same force continues to act afterwards. The coefficient of the static friction and sliding friction are $0.5$ and $0.4$ respectively. The acceleration of the body is:
(A) $9.8\,{\text{m}}{{\text{s}}^{ - 2}}$
(B) $3.2\,{\text{m}}{{\text{s}}^{ - 2}}$
(C) $1\,{\text{m}}{{\text{s}}^{ - 2}}$
(D) $5\,{\text{m}}{{\text{s}}^{ - 2}}$

Answer 1

First of all, we will find the limiting friction and the kinetic friction separately. Then we will find out the net accelerating force by subtracting these two quantities. We will find the acceleration by using Newton’s second law of motion.

Complete step by step answer:
In the given question, we are provided with the following data:
The mass of the body is $60\,{\text{kg}}$ .
The coefficient of the static friction and sliding friction are $0.5$ and $0.4$ respectively.
We are asked to find the acceleration of the body.
For better understanding, we draw a diagram which shows all the forces acting on the body. The weight of the body acts in the downward direction. The normal reaction acts upwards. The force applied acts towards right.

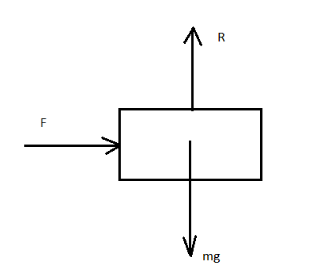
First, we will find the limiting friction, which is given by the formula:
${F_{\text{l}}} = {\mu _{\text{s}}}R$ …… (1)
Where,
${F_{\text{l}}}$ indicates limiting friction.
${\mu _{\text{s}}}$ indicates coefficient of the static friction.
$R$ indicates normal reaction.
Substituting the required values in the equation (1), we get:

$${F_{\text{l}}} = {\mu _{\text{s}}}R \\\ {F_{\text{l}}} = {\mu _{\text{s}}}mg \\\ {F_{\text{l}}} = 0.5 \times 60 \times 10\,{\text{N}} \\\ {F_{\text{l}}} = 300\,{\text{N}} \\\$$

The value of limiting friction is found to be $300\,{\text{N}}$ .
For the second case, we find the kinetic friction:
${F_{\text{k}}} = {\mu _{\text{k}}}mg$ …… (1)
Where,
${F_{\text{k}}}$ indicates kinetic friction.
${\mu _{\text{k}}}$ indicates coefficient of the kinetic friction.
$mg$ indicates weight force.
Substituting the required values in the equation (1), we get:

$${F_{\text{k}}} = {\mu _{\text{k}}}mg \\\ {F_{\text{k}}} = 0.4 \times 60 \times 10\,{\text{N}} \\\ {F_{\text{k}}} = 240\,{\text{N}} \\\$$

The value of kinetic friction is found to be $240\,{\text{N}}$ .
The force applied force is $300\,{\text{N}}$ .
So, we need to find the net accelerating force which is the difference of limiting friction and the kinetic friction.
So, we can write:
$F = {F_{\text{l}}} - {F_{\text{k}}}$ …… (2)
Where,
$F$ indicates the net accelerating force.
${F_{\text{l}}}$ indicates the limiting force.
${F_{\text{k}}}$ indicates the kinetic friction.
Substituting the required values in the equation (2), we get:

$$F = {F_{\text{l}}} - {F_{\text{k}}} \\\ ma = 300 - 240 \\\ a = \dfrac{{60}}{{60}} \\\ a = 1\,{\text{m}}{{\text{s}}^{ - 2}} \\\$$

Hence, the acceleration of the body is found to be $1\,{\text{m}}{{\text{s}}^{ - 2}}$ .
The correct option is C..

Note: While solving this problem, we need to understand that limiting friction is different from kinetic friction. Limiting friction is the maximum friction that is generated between two static surfaces which are in contact. Kinetic friction is that force which acts between two surfaces when they are moving.