Question

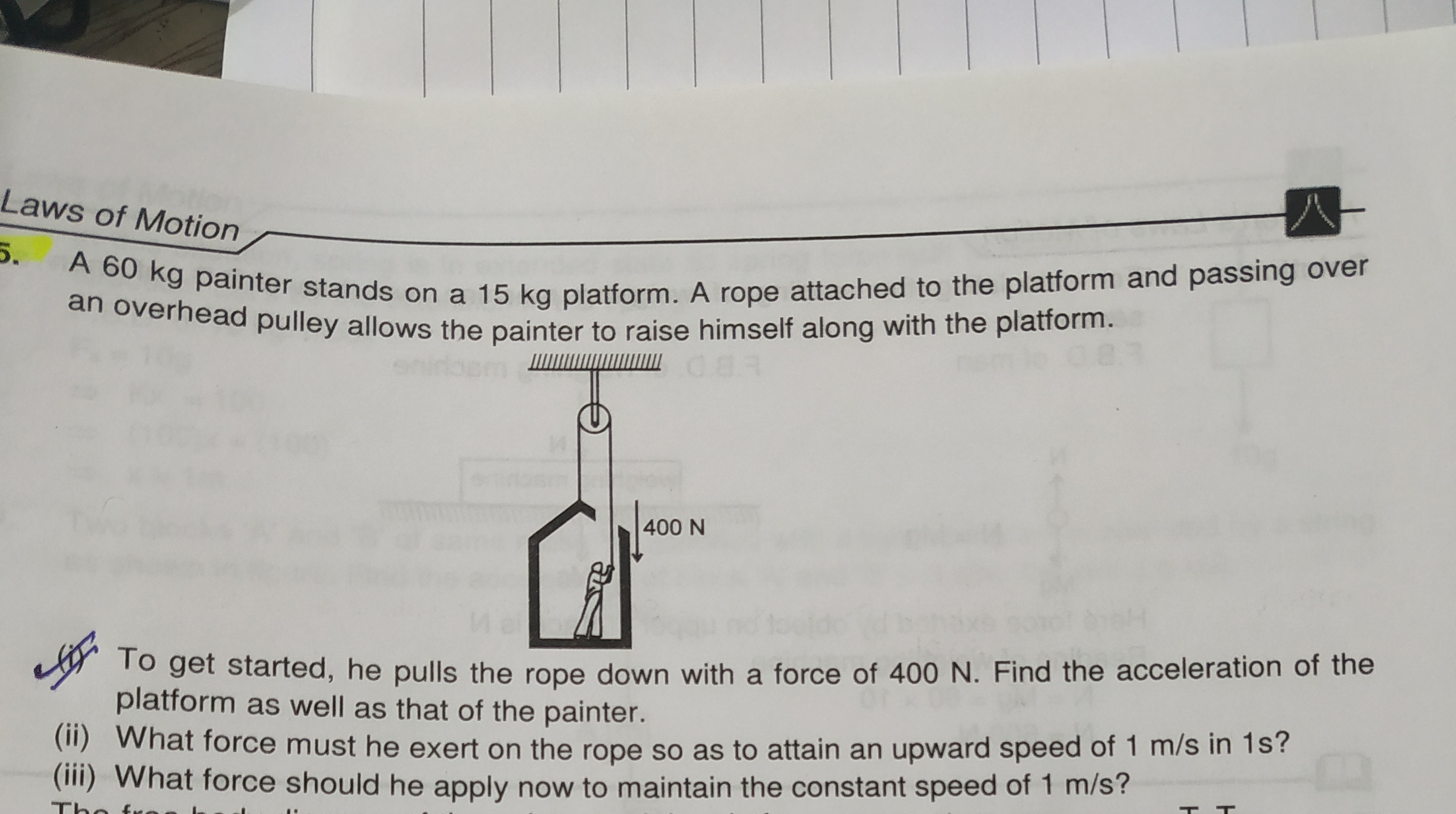
A 60 kg painter stands on a 15 kg platform. A rope attached to the platform and passing over an overhead pulley allows the painter to raise himself along with the platform.

To get started, he pulls the rope down with a force of 400 N. Find the acceleration of the platform as well as that of the painter.

(ii) What force must he exert on the rope so as to attain an upward speed of 1 m/s in 1s?

(iii) What force should he apply now to maintain the constant speed of 1 m/s?

Answer 1

(i) The acceleration of the platform and the painter is $\frac{2}{3} \, m/s^2$ upwards. (ii) The force he must exert on the rope is 412.5 N. (iii) The force he should apply now to maintain the constant speed is 375 N.

Answer 2

Let $M_p$ be the mass of the painter and $M_{pl}$ be the mass of the platform.

$M_p = 60$ kg $M_{pl} = 15$ kg

The total mass of the system (painter + platform) is $M = M_p + M_{pl} = 60 + 15 = 75$ kg.

Let $F$ be the force with which the painter pulls the rope downwards. Due to the pulley system configuration, there are two segments of the rope pulling upwards on the combined system: one segment attached to the platform and the segment held by the painter. The tension in the rope is equal to the force $F$ exerted by the painter. Thus, the total upward force on the system is $2F$.

The downward force on the system is its weight, $W = Mg$.

Let $a$ be the upward acceleration of the system.

Applying Newton's second law to the system (taking upward direction as positive):

$2F - Mg = Ma$ $2F - (M_p + M_{pl})g = (M_p + M_{pl})a$

Using $g = 10 \, m/s^2$.

$2F - 75(10) = 75a$ $2F - 750 = 75a$

(i) To find the acceleration when the painter pulls with a force of 400 N:

Given $F = 400$ N.

Substitute this value into the equation:

$2(400) - 750 = 75a$ $800 - 750 = 75a$ $50 = 75a$ $a = \frac{50}{75} = \frac{2}{3} \, m/s^2$.

The acceleration of the platform and the painter is $\frac{2}{3} \, m/s^2$ upwards.

(ii) To find the force required to attain an upward speed of 1 m/s in 1s:

Assume the system starts from rest, so initial velocity $u = 0$.

Final velocity $v = 1$ m/s.

Time $t = 1$ s.

The required upward acceleration is $a = \frac{v - u}{t} = \frac{1 - 0}{1} = 1 \, m/s^2$.

Substitute this value of $a$ into the equation of motion:

$2F - 750 = 75a$ $2F - 750 = 75(1)$ $2F - 750 = 75$ $2F = 750 + 75$ $2F = 825$ $F = \frac{825}{2} = 412.5$ N.

The force he must exert on the rope is 412.5 N.

(iii) To find the force required to maintain a constant speed of 1 m/s:

Maintaining a constant speed means the acceleration is zero, $a = 0$.

Substitute this value of $a$ into the equation of motion:

$2F - 750 = 75a$ $2F - 750 = 75(0)$ $2F - 750 = 0$ $2F = 750$ $F = \frac{750}{2} = 375$ N.

The force he should apply is 375 N.

Explanation of the solution:

The system consists of the painter and the platform, moving together with total mass $M = 75$ kg. Two segments of the rope exert upward tension on the system, each equal to the force $F$ the painter pulls with. The total upward force is $2F$. The downward force is the weight $Mg$. Applying Newton's second law, $2F - Mg = Ma$. Using $g=10 \, m/s^2$, the equation is $2F - 750 = 75a$.

(i) For $F=400$ N, solve for $a$: $2(400) - 750 = 75a \implies 50 = 75a \implies a = 2/3 \, m/s^2$.

(ii) To attain $v=1 \, m/s$ in $t=1 \, s$ from rest, $a = 1 \, m/s^2$. Solve for $F$: $2F - 750 = 75(1) \implies 2F = 825 \implies F = 412.5$ N.

(iii) To maintain constant speed, $a=0$. Solve for $F$: $2F - 750 = 75(0) \implies 2F = 750 \implies F = 375$ N.