Question

A $60\,kg$ man is inside a lift which is moving up with an acceleration of $2.45\,m{s^{ - 2}}$. The apparent percentage change in his weight is:
A. 20%
B. 25%
C. 50%
D. 75%

Answer 1

It is a lift – acceleration problem with lift moving in upward direction. Before starting the solution, one must be clear about the direction of forces acting on the body inside lift, so that one can easily equate the forces. Besides this one must be aware about weight and what it actually is.

Complete step by step answer:
Weight of the body is the normal force it exerts on the ground. Generally, gravity is the only force which balances this normal force so we consider the force by gravity as the weight of the body and in presence of other forces the weight is called the apparent weight of the body.

In equations of lift, weight of man is the normal force the man exerts on the ground of lift which is also the apparent weight of man. If the lift is accelerating in any direction, then the net force that acts on man is not one by gravity but also the force by accelerating lift. In above question the lift is accelerating in upward direction:
Assume apparent weight of man in lift = W
Net acceleration of system = acceleration of lift = $2.45\,m{s^{ - 2}}$ = ${a_{net}}$

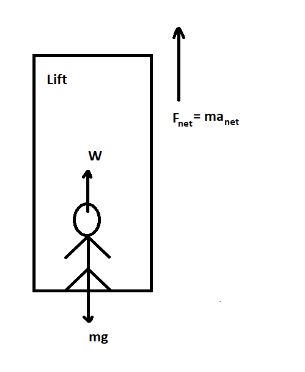
Forces acting in upward direction are the weight of man and the net acceleration of the system.Equating all the forces of the system,
$W - mg = m{a_{net}}$
Where, $m$ = mass of man, $g$ = acceleration due to gravity
Putting value of variables from question,
$W - \left( {60 \times 9.8} \right) = 60 \times 2.5$
$\Rightarrow W - 588 = 150$
Evaluating the equation to know the apparent weight of man,
$W = 738\,N$
Actual weight of body = $mg$
${\text{Actual}}\,{\text{weight}} = 60 \times 9.8 = 588\,N$

Change in weight = apparent weight – actual weight
Change in weight = 738 – 588 = 150 N
${\text{Percentage change}} = \dfrac{{{\text{Change in weight}}}}{{{\text{Actual weight}}}} \times 100$
Evaluating above equation by putting values in equation,
{\text{% change}} = \dfrac{{150}}{{588}} \times 100
Substituting above values will give,
$\% \text{change} = 25\%$
When lift is accelerating upward with $2.45\,m{s^{ - 2}}$ acceleration, the apparent percentage change in weight of man is 25%.

Therefore, the correct answer is option B.

Note: Lift – acceleration system generates 3 situations. One in which lift is accelerating upward (the one we studied). Second case is when lift is accelerating downward and in the third case there is no acceleration in lift. We must carefully understand the situation and use the respective method in solving the problems.