Solveeit Logo
Login

Question

Question: A 60 kg man holding a \(20kg\) box rides on a skateboard at a speed of \(7m{s^{ - 1}}\). He throws t...

A 60 kg man holding a 20kg20kg box rides on a skateboard at a speed of 7ms−17m{s^{ - 1}}. He throws the box behind him, giving it a velocity of 5ms−15m{s^{ - 1}}. with respect to the ground. What is his velocity after throwing the object?

A) 8ms−18m{s^{ - 1}}
B) 9ms−19m{s^{ - 1}}
C) 10ms−110m{s^{ - 1}}
D) 11ms−111m{s^{ - 1}}
E) 12ms−112m{s^{ - 1}}

Explanation

Solution

The problem is based on the concept of conservation of momentum of the system. Now the conservation of momentum states that, the initial total momentum of the system = the final total momentum of the system.

Complete step by step solution:
Step 1:

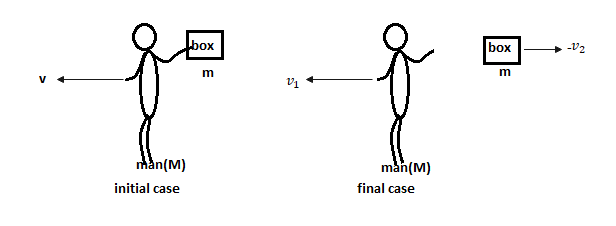
We consider the direction of the man’s motion is the positive direction.
In the initial position man of massMMholding the box of mass. And going in a positive direction and then he threw the box behind him. That means the box’s final motion is in the negative direction but the man’s final motion is in the positive direction. Therefore from the conservation of linear momentum we get,
(M+m)v=Mv1+m(−v2)\left( {M + m} \right)v = M{v_1} + m\left( { - {v_2}} \right)------------------------ (1 )
where, v=v = the velocity of the man and box initially,v1={v_1} = the velocity of the man after throw the box behind him, −v2=- {v_2} = the velocity of the man after throw the box in final case as it going in negative direction.
Step2: According to the question the,v=7ms−1v = 7m{s^{ - 1}}, −v2=−5ms−1 - {v_2} = - 5m{s^{ - 1}}, M=60kgM = 60kg, m=20kgm = 20kg.
Then from equation (1) we get,
⇒(M+m)v=Mv1+m(−v2)\Rightarrow \left( {M + m} \right)v = M{v_1} + m\left( { - {v_2}} \right)
⇒(60+20)7=60v1+20(−5)\Rightarrow \left( {60 + 20} \right)7 = 60{v_1} + 20\left( { - 5} \right)
⇒80×7=60v1−100\Rightarrow 80 \times 7 = 60{v_1} - 100
⇒60v1=560+100\Rightarrow 60{v_1} = 560 + 100
⇒v1=66060\Rightarrow {v_1} = \dfrac{{660}}{{60}}
∴v1=11ms−1\therefore {v_1} = 11m{s^{ - 1}}
Therefore, the velocity of the man after throwing the object is11ms−111m{s^{ - 1}}.
∴\therefore The correct option is option (D).

Note: student must notice carefully that we use the velocity of the man and the box as a vector quantity. That’s why we use positive and negative direction for the man and the box velocity respectively.
We always use a vector sum for the conservation of momentum equation.