Question
Question: A \(60\,cm\) long wire (mass 10 g) is hanged by two flexible wires in a magnetic field of \(0.40\,T\...
A 60cm long wire (mass 10 g) is hanged by two flexible wires in a magnetic field of 0.40T. Find the magnitude and direction of the current required to be flown to neutralize the tension of the hanging wires.
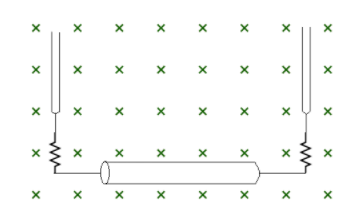
Solution
To neutralize the tension of the hanging wires, a force needs to be applied in the opposite direction of the hanging wire and that force should be equal to the tension of the hanging wire.
Formula used:
F=IlB, where I is magnitude of current,
l is length of wire, and
B is the magnetic field.
Complete step by step answer:
According to the question, we know that –
m=10g=10−2kg, l=60cm=0.6m and B=0.40T
The tension on the hanging wire is mainly due to the gravitational force, i.e., mgand the force should be equal to this gravitational force, that will neutralize the tension on the hanging wires.
∴F=mg
And, we know that magnetic force is represented as:
F=IlB
Hence,
IlB=mgI×0.6×0.40=10−2×9.8I=0.240.098I=0.41A
And, the direction of current should be from left to right, so that the magnetic force that is applied in the hanging wire is upward, to counter the tension of the hanging wire.
Therefore, the correct value of current is 0.41A and the direction of current is left to right.
Note:
Students should have a good understanding of the force that is being applied on a body in magnetic force. In this question, we can say that the tension on the wire was equal to the gravitational force, because nothing was explicitly mentioned in the question.
