Question

A 60.0 kg wagon experiences a variable net force in the forward direction according to the graph pictured below. If it starts from rest, what is its speed after 9 second?

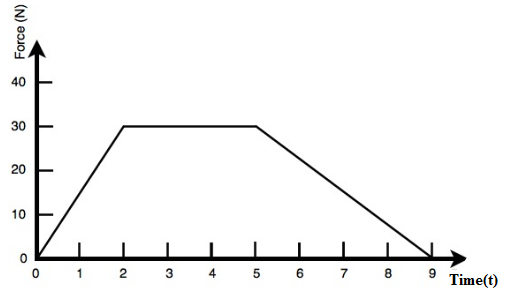
A. 3.0 m/s
B. 6.67 m/s
C. 3.33 m/s
D. 5.3 m/s
E. 1.7 m/s

Answer 1

Use Newton’s second law of motion to determine the relation between velocity of wagon and area under the curve. To calculate the area under the curve, divide the curve in three parts including two triangles and one rectangle and sum up the areas.

Formula used:
$F = m\dfrac{{dv}}{{dt}}$
Here, m is the mass and v is the velocity.

Complete step by step answer:
We have according to Newton’s second law of motion, the force is given as,
$F = m\dfrac{{dv}}{{dt}}$
$\Rightarrow dv = \dfrac{1}{m}Fdt$
We can integrate the above equation from time 0 to t second as follows,
$v = \dfrac{1}{m}\int\limits_0^t {Fdt}$
The term of integration in the above equation represents the area under the curve of F-t graph. Therefore, we substitute A for $\int\limits_0^t {Fdt}$ in the above equation.
$v = \dfrac{A}{m}$
Therefore, from the above equation we can conclude that the velocity of the wagon is the area under the curve of Force and time divided by the mass of the wagon.
The area covered by the F-t graph consists of two triangles and one rectangle as shown in the figure below.

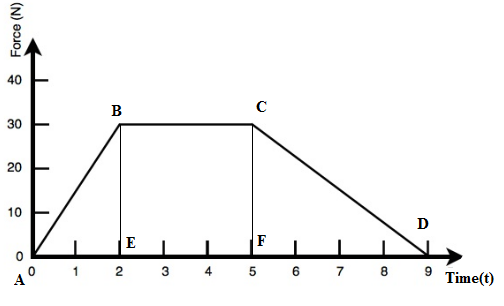
We can see the area under the F-t curve is the sum of area of triangle ABE, area of triangle CFD and area of rectangle BCFE. Therefore,
$A = \dfrac{1}{2}\left( {30 \times 2} \right) + \dfrac{1}{2}\left( {30 \times 4} \right) + \left( {30 \times 3} \right)$
$\Rightarrow A = 30 + 60 + 90$
$\Rightarrow A = 180\,$
Therefore, we have the velocity of the wagon after 9 s is,
$v = \dfrac{A}{m}$
Substitute 180 for A and 60 kg for m in the above equation.
$v = \dfrac{{180}}{{60}}$
$\Rightarrow v = 3.0\,m/s$

So, the correct answer is “Option A”.

Note:
While solving such types of questions you should always check the units of given quantities. If the given quantities are in a CGS unit, you should convert it in S.I. units. In such types of questions, you always need to calculate the area under the curve. If you were asked to determine the velocity of the wagon after 5 second, you should calculate the area under the curve of the first triangle and the rectangle.