Solveeit Logo
Login

Question

Question: A 6 kg weight is fastened to the end of a steel wire of unstretched length 60 cm. It is whirled in a...

A 6 kg weight is fastened to the end of a steel wire of unstretched length 60 cm. It is whirled in a vertical circle and has an angular velocity of 2 rev/s at the bottom of the circle. The area of the cross section of the wire is0.05cm20.05c{m^2}. Calculate the elongation of the wire when the weight is at the lowest point of the path. Young’s modulus of steel=2×1011N/m2 = 2 \times {10^{11}}N/{m^2}

Explanation

Solution

The elasticity of the string will cause it to stretch and regain its original shape due to the circular motion and the weight attached to it. Young’s modulus is given by the ratio of normal stress to longitudinal strain. Thus, Young’s modulus is inversely proportional to the change in length of the string.

Formula Used: Young’s modulus of a material is given by: Y=σnεl=T×LA×lY = \dfrac{{{\sigma _n}}}{{{\varepsilon _l}}} = \dfrac{{T \times L}}{{A \times l}}

Complete step by step solution: It the problem that a string is whirled in vertical direction with the given data:

Mass attached to the string=m=6kgm = 6kg
Length of the string=L=60cm=0.6mL = 60cm = 0.6m

Angular velocity at the bottom of the circle=ω\omega =2 rev/s=2π×2=4π rad/sec2\pi \times 2 = 4\pi {\text{ rad/sec}}

Area of cross section of the wire=0.05cm2=0.05×10−4m20.05c{m^2} = 0.05 \times {10^{ - 4}}{m^2}

Young’s modulus of steel=2×1011N/m2 = 2 \times {10^{11}}N/{m^2}

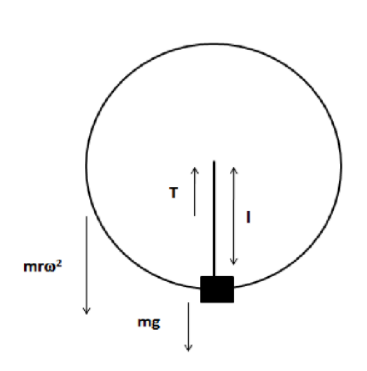
Consider the position of the wire when the weight attached to it is at the lowest point of the circle when whirled vertically. As seen in the diagram, the weight of the object mgmg and the centrifugal force

mrω2mr{\omega ^2}will act vertically downwards (where, mmis the mass, ggis the gravitational
acceleration, rr is the radius of the circle and ω\omega is the angular velocity). The tension TTin the string will act vertically upwards.

Balancing the forces acting upwards and downwards on the string.

\therefore T = m\left( {r{\omega ^2} + g} \right) \\\ \therefore T = 6\left[ {(0.6 \times {{(4\pi )}^2}) + 9.8} \right] \\\ \therefore T = 6\left[ {(94.7482) + 9.8} \right] \\\ \therefore T = 6\left[ {104.5482} \right] \\\ \therefore T = 627.2892 \\\ \therefore T = 627N \\\ \ $$ The ratio of the normal stress $${\sigma _n}$$ to the longitudinal strain$${\varepsilon _l}$$ is called as Young’s modulus $$Y$$. Thus, $$Y = \dfrac{{{\sigma _n}}}{{{\varepsilon _l}}} = \dfrac{{T \times L}}{{A \times l}}$$ where, $$l$$ is the change in length. Therefore above equation can be rearranged as $$\ l = \dfrac{{T \times L}}{{A \times Y}} \\\ \therefore l = \dfrac{{627 \times 0.6}}{{\left( {0.05 \times {{10}^{ - 4}}} \right) \times \left( {2 \times {{10}^{11}}} \right)}} = \dfrac{{376.2}}{{0.1 \times {{10}^7}}} = 3762 \times {10^{ - 7}} = 3.8 \times {10^{ - 4}}m \\\ \ $$ $$$$ **Therefore, the elongation of the wire when the weight is at lowest point of the path is $$3.8 \times {10^{ - 4}}$$meters.** **Note:** A steel wire of a certain length and certain cross section is whirled in a vertical circle. In that case, the elongation of the wire will be the maximum when the weight attached to it is at the lowest point of the circle and will be minimum when it is at the highest point of the circle.