Question

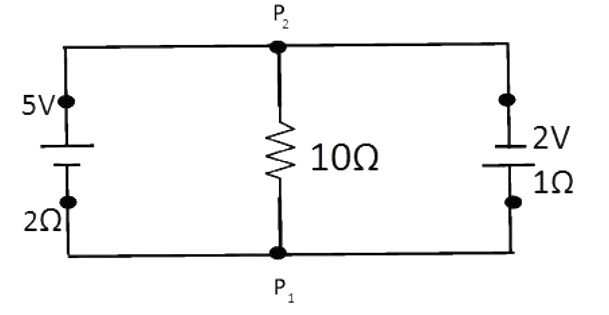
A $5V$ battery with internal resistance $2\Omega$ and a $2V$ battery with internal resistance $1\Omega$ are connected to a $10\Omega$ resistor as shown in figure, the current in the $10\Omega$ resistor is?

A. $0.27A$
B. $0.31A$
C. $0.031A$
D. $0.53A$

Answer 1

In order to answer the given question we need to apply the voltage-current relation from Ohm’s law in the given circuit. Also, we need to apply Kirchhoff’s law to the loops in the given circuit. After that we need to solve the obtained equations and finally conclude with the solution of the given question. Therefore, we need to solve the equation formed to conclude with the solution.

Complete step by step answer:
Let us redraw the circuit and name the loops in the given circuit.
Also let us assume that current ${I_1}$ is flowing through the $10\Omega$ resistor.
And current flowing through ${P_2}B$ be $I - {I_1}$
Now we need to apply KVL to the closed loop $A{P_2}{P_1}CA$
$- 10{I_1} - 2I + 5 = 0$
$\Rightarrow 2I + 10{I_1} = 5............(i)$

Similarly by applying KVL to the closed loop ${P_2}BD{P_1}{P_2}$ , we get,
$2 - 1(I - {I_1}) + 10y = 0$
$\Rightarrow I - 11{I_1} = 2...........(ii)$

Now on multiplying equation (ii) by $2$ we get,
$2I - 22{I_1} = 4$ …………..(iii)
Step four
Now, we need to subtract equation (iii) from equation (i)
By doing so, we get,
$32{I_1} = 1$
$\Rightarrow {I_1} = \dfrac{1}{{32}} = 0.031A$
Therefore, the required amount of current that is flowing through the $10\Omega$ resistance is $0.031A$ .

Hence, the correct answer is option (C).

Note: There are two rules according to Kirchhoff’s law. One is Kirchhoff voltage law (KVL) and the other is Kirchhoff’s current law (KCL). According to KVL the sum of all the potential in a closed loop is zero. Similarly according to KCL the sum of all the current in a closed loop is zero. Both KVL and KCL follow the conservation of energy across a closed loop or path.