Question

A 50kg person stands on a 25kg platform. He pulls on the rope which is attached to the platform via frictionless pulleys as shown in the figure. The platform moves upward at a steady rate. The force with which the person pulls the rope is:

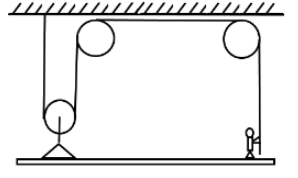
A. 500N
B. 250N
C. 25N
D. 50N

Answer 1

It is mentioned in the question that the platform moves with a steady rate which implies that the change in velocity with respect to time is zero i.e. the acceleration of the platform is zero. Therefore we can say that the net force on the platform will be equal to zero. Applying Newton's law of motion to write the equation for force on the platform and then equating it to zero gives us the force with which the man pulls the rope.

Complete step by step answer:
Given mass of man, $m = 50kg$, Mass of platform, $M = 25kg$

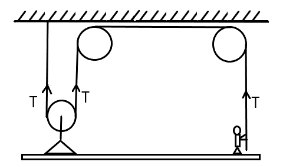
The free body diagram for the platform is

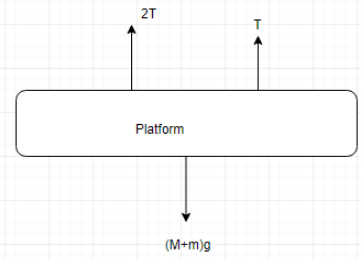
The equation of force, F for the platform is,
$3T - (m + M)g = F$
Given in the question that the platform moves with steady rate which implies the change in the velocity of the platform with respect to time is zero, implies the force on the platform is zero, $F = 0$
$3T - \left( {m + M} \right)g = 0 \\\ \Rightarrow 3T = \left( {m + M} \right)g \\\$
Substituting the value of m and M, we get
$3T = \left( {50 + 25} \right)10 \\\ \Rightarrow T = \dfrac{{750}}{3} = 250N$
This tension (T) is equal to the force applied by the man on the rope to pull the platform =250N.

Therefore the force by which the man should pull the rope for the platform to move at a steady rate is 250N.

Note: Students should draw correct free body diagrams to obtain correct equations for solving this question. It is important to understand the meaning of steady rate, which implies no change in the velocity with respect to the time.