Question
Question: A \(50kg\) homogeneous smooth sphere rests on the \({{30}^{o}}\) inclined plane at A and bears again...
A 50kg homogeneous smooth sphere rests on the 30o inclined plane at A and bears against the smooth vertical wall B. Calculate the contact forces at A and B.
Solution
A sphere is in contact with an inclined plane and a wall and is at rest. This means that the forces acting on the system cancel each other and there is no external force acting on the system. On resolving the forces along the axes, we can find relationships between forces and use it to calculate the normal reactions acting on the spheres.
Formulas used:
mg=N1sin30o
N2=N1cos30o
Complete step-by-step solution:
As there is no external force acting on the sphere, the system is isolated. The sphere is at rest on the inclined plane and against the wall. The contact forces, also called normal forces are forces exerted by one surface over the other so as to prevent the surface from passing through it. The forces acting on it will be-
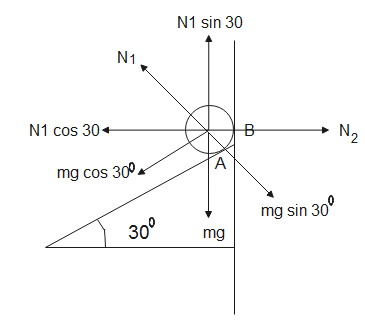
By resolving different internal forces acting on the sphere, we get the following relations,
mg=N1sin30o - (1)
Here,
m is the mass of the sphere
g is acceleration due to gravity
N1 is the contact force acting between the sphere and the inclined plane
N2=N1cos30o - (2)
N2 is the contact force between wall and sphere
When we substitute given values in eq (1), we get,
50×10=N1×21∴N1=1000N
We substitute the value from the above equation to get,
N2=1000×23∴N2=5003N
The contact forces acting between the incline and sphere is 1000N and the contact forces acting between the wall and sphere is 5003N.
Note:
By Newton’s third law of motion, the normal forces are equal and opposite in nature and are perpendicular to the surfaces. The components of a force are perpendicular to each other. Smooth surface means that there is no friction. Since it is an isolated system, the sphere will remain at rest unless an external force is applied on it.
