Question

A 5000kg rocket is set for a vertical firing. The exhaust speed is 800m/s. To give an upward acceleration of $20m{{s}^{-2}}$ the amount of gas ejected per second to supply the needed thrust is ($g=10m{{s}^{-2}}$)
$\begin{aligned} & a)127.5kg{{s}^{-1}} \\\ & b)137.5kg{{s}^{-1}} \\\ & c)187.5kg{{s}^{-1}} \\\ & d)185.5kg{{s}^{-1}} \\\ \end{aligned}$

Answer 1

A rocket works on the principle of law of conservation of momentum. The fuel continuously gets ejected from the rocket as a result an upward thrust is generated which helps the rocket to propel. Now we want the rocket to move with an upward acceleration of $20m{{s}^{-2}}$ which is the net acceleration. The thrust force on the rocket comprises the terms i.e. fuel ejected per unit time. Hence using the equation of net force on the rocket such that it is moving with acceleration of $20m{{s}^{-2}}$, we can calculate the gas ejected per second to supply the needed thrust.

Complete step-by-step answer:

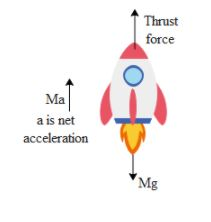
In the above free body diagram we can see that the thrust force gives a net acceleration upwards to the rocket. The mass of the rocket is M, hence the gravitational force acts vertically downwards. Hence the equation of motion of the rocket is,
${{F}_{NET}}={{F}_{THRUST}}-{{F}_{GRAVITY}}...(1)$.
Let us say the rocket moves vertically upwards with acceleration a, hence the net force on the rocket is ${{F}_{NET}}=Ma$ The thrust force acting on the rocket is given by, ${{F}_{THRUST}}={{U}_{REL}}\dfrac{dm}{dt}$ where ${{U}_{REL}}$is the relative velocity of the rocket with respect to the ejected gas and $\dfrac{dm}{dt}$is the rate at which the fuel gets ejected from the rocket.
Let us now use equation 1 to determine the term i.e. $\dfrac{dm}{dt}$gas ejected per sec.
$\begin{aligned} & {{F}_{NET}}={{F}_{THRUST}}-{{F}_{GRAVITY}} \\\ & \Rightarrow Ma={{U}_{REL}}\dfrac{dm}{dt}-Mg \\\ & \Rightarrow Ma+Mg={{U}_{REL}}\dfrac{dm}{dt} \\\ & \Rightarrow \dfrac{dm}{dt}=\dfrac{M(a+g)}{{{U}_{REL}}} \\\ & \Rightarrow \dfrac{dm}{dt}=\dfrac{5000(20+10)}{800}=\dfrac{500(3)}{8}=187.5kg{{s}^{-1}} \\\ \end{aligned}$

So, the correct answer is “Option C”.

Note: The exhaust speed is always given relative to the rocket. The faster we accelerate the rocket more fuel has to be burnt per sec. Once the entire fuel is consumed the speed acquired by the rocket is called the burnout speed. This is the maximum speed a rocket can have and is directly proportional to the exhaust speed of the rocket.