Question: There are two identical spheres, (I) Hangs by thermally insulated wire and (II) is placed on thermal...

Question

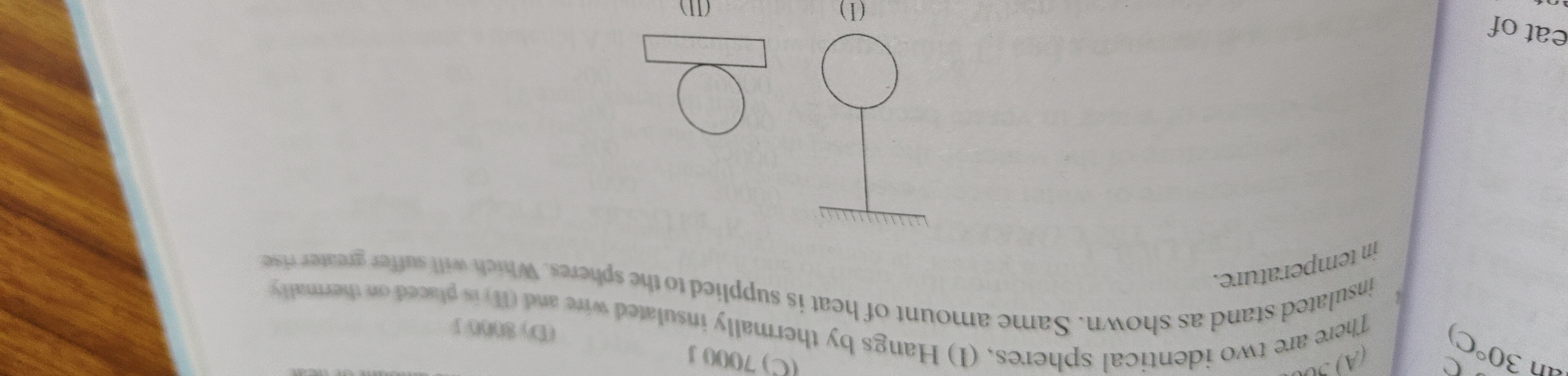
There are two identical spheres, (I) Hangs by thermally insulated wire and (II) is placed on thermally insulated stand as shown. Same amount of heat is supplied to the spheres. Which will suffer greater rise in temperature.

Answer 1

Solution

The rise in temperature ( $\Delta T$ ) of an object when heat ( $Q$ ) is supplied is given by the formula $Q = mc\Delta T$ , where $m$ is the mass and $c$ is the specific heat capacity. Thus, $\Delta T = \frac{Q}{mc}$ .

We are given that the two spheres are identical, so they have the same mass ( $m$ ) and the same specific heat capacity ( $c$ ). The same amount of heat ( $Q$ ) is supplied to both.

Sphere (I) hangs by a thermally insulated wire, so heat loss through the wire is minimized. Its entire surface area is exposed to the surroundings, leading to heat loss by convection and radiation. Sphere (II) is placed on a thermally insulated stand. The stand minimizes heat loss by conduction. However, the sphere is in contact with the stand, which reduces the surface area available for heat loss by convection and radiation compared to sphere (I).

Let $A_1$ be the total surface area of sphere (I) and $A_2$ be the exposed surface area of sphere (II). Due to the contact with the stand, $A_2 < A_1$ . The rate of heat loss is proportional to the exposed surface area. Therefore, the heat lost by sphere (II) ( $Q_{lost, II}$ ) is less than the heat lost by sphere (I) ( $Q_{lost, I}$ ).

The net heat absorbed by the sphere is $Q_{net} = Q_{supplied} - Q_{lost}$ . The temperature rise is $\Delta T = \frac{Q_{net}}{mc}$ . Since $Q_{supplied}$ is the same for both spheres, and $Q_{lost, II} < Q_{lost, I}$ , it follows that $Q_{net, II} > Q_{net, I}$ . Consequently, $\Delta T_{II} > \Delta T_{I}$ . Sphere (II) will suffer a greater rise in temperature.