Question

A $50\,g$of ${{H}_{2}}$is placed in a vessel of constant volume and temperature. A hole is punctured in the vessel and left in vacuum. The pressure of ${{H}_{2}}$in the vessel will vary with time as:
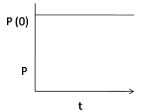
1.
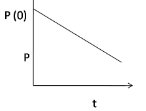
2.
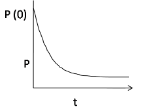
3.
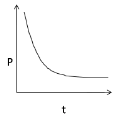
4.

Answer 1

The pressure and time variant will be obtained from the diffusion rate of the hydrogen gas in that vessel. As the time changes the diffusion of this gas starts taking place.

Complete step by step solution:
When a gas is kept in a vessel at constant temperature and volume, and a hole is punctured into it and then kept in vacuum, then due to the kinetic energy of gaseous particles the movement of the gas occurs from the vessel into vacuum, this is called diffusion.
The rate of diffusion of gases involves the number of moles of gas diffused upon the time taken by the gas for diffusion or movement as:
Rate of diffusion of gas $=\dfrac{number\,of\,moles\,diffused}{time\,taken}$
When some pressure is introduced, then this rate becomes directly proportional with pressure of the gas, as the pressure increases, the kinetic energy of the gas particles increases and hence, the rate of diffusion increases as the particles move more fast. So, the relation of rate of diffusion with pressure is:
$rate\,of\,diffusion\,of\,gas\,\propto \,pressure$
So, through this relation, the pressure will be inversely proportional to time taken by the gas as:
$~$
$rate\,of\,diffusion\,of\,gas=\dfrac{moles\,diffused}{time\,taken}\,\propto \,pressure$
Therefore, when moles start to diffuse with time, the pressure is decreased.

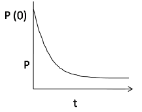
At P(0), the pressure is maximum when the hole is just punctured, gradually it decreases with time, hence option (3) is correct.

Note: The rate of diffusion of Graham’s law is that the diffusion rate is inversely proportional to square root of molar mass of the gas. This law along with the ideal gas equation $PV=nRT$, derives this rate of diffusion to be directly proportional to pressure of the gas.