Question

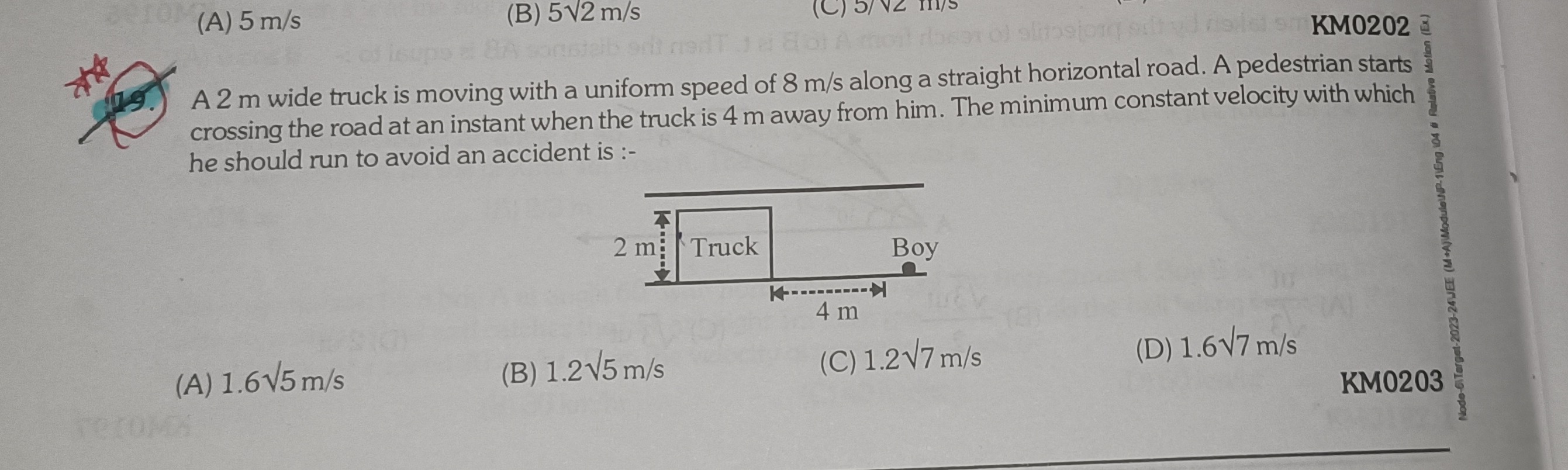
A 2 m wide truck is moving with a uniform speed of 8 m/s along a straight horizontal road. A pedestrian starts crossing the road at an instant when the truck is 4 m away from him. The minimum constant velocity with which he should run to avoid an accident is :-

• A. 1.6√5 m/s
• B. 1.2√5 m/s
• C. 1.2√7 m/s
• D. 1.6√7 m/s

Answer 1

Answer: (A)

1.6√5 m/s

Answer 2

Let the pedestrian cross the road of width 2m with velocity $v$ at an angle $\phi$ with the road. The component of velocity perpendicular to the road is $v \sin\phi$, and the component parallel to the road is $v \cos\phi$. The time taken to cross the road is $t = \frac{2}{v \sin\phi}$. During this time, the pedestrian covers a distance $x_p = v \cos\phi \cdot t = v \cos\phi \cdot \frac{2}{v \sin\phi} = 2 \cot\phi$ along the road. The truck is moving at 8 m/s and is initially 4 m away. For safe crossing, the pedestrian must reach the other side of the road at time $t$ such that the truck has covered a distance of at least $4 + x_p = 4 + 2 \cot\phi$. The time taken by the truck to cover this distance is $\frac{4 + 2 \cot\phi}{8}$. For safe crossing, the time taken by the pedestrian must be less than or equal to the time taken by the truck to reach the point the pedestrian aims for: $\frac{2}{v \sin\phi} \le \frac{4 + 2 \cot\phi}{8}$. Simplifying this inequality gives $v \ge \frac{16}{4 \sin\phi + 2 \cos\phi}$. To find the minimum velocity, we maximize the denominator $4 \sin\phi + 2 \cos\phi$, which has a maximum value of $\sqrt{4^2 + 2^2} = \sqrt{20} = 2\sqrt{5}$. Thus, the minimum velocity is $v_{min} = \frac{16}{2\sqrt{5}} = \frac{8}{\sqrt{5}} = 1.6\sqrt{5}$ m/s.