Question

A 5 meter long ladder is resting against a vertical wall. At the moment when the foot of the ladder is 3 meter from the wall it starts sliding away from the wall at the rate of 0.5m/sec. The rate at which the angle between the floor and the ladder is decreasing is
(a) $\dfrac{1}{8}$ rad/sec
(b) $\dfrac{1}{4}$ rad/sec
(c) $\dfrac{1}{6}$ rad/sec
(d) $\dfrac{1}{16}$ rad/sec

Answer 1

We will construct a rough diagram using the given information. Then, we will look at the equation that will relate the angle between the ladder and the floor to the distance of the foot of the ladder from the wall. We will use differentiation to get an equation that will give us a relation between the rate at which the ladder is sliding and the rate at which the angle between the floor and the ladder is decreasing. Solving these equations will lead us to the answer.

Complete step by step answer:
Let us construct a rough diagram.

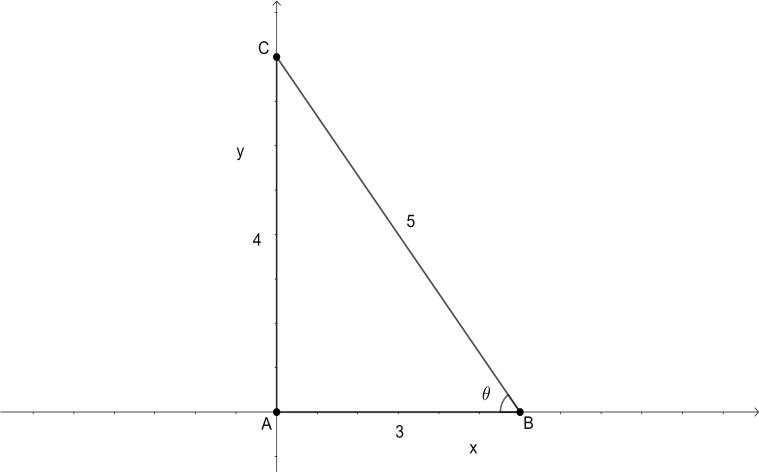
We have a right angled triangle with sides having length 3 and 5 m. Using the Pythagoras theorem, we get the third side as 4 m. The length of the hypotenuse, which is the ladder, will always be constant (5 m), even when the ladder is sliding. Let the angle between the ladder and the ground be $\theta$. Now, we will look at an equation that will relate $x$ and $\theta$. We know that $\cos \theta =\dfrac{\text{Adjacent}}{\text{Hypotenuse}}$ .
Therefore, we have $\cos \theta =\dfrac{x}{5}$ . Now, let the rate at which the ladder is sliding be $\dfrac{dx}{dt}$ and the rate of change in the angle between ladder and ground be $\dfrac{d\theta }{dt}$. To get a relation between $\dfrac{dx}{dt}$ and $\dfrac{d\theta }{dt}$, we will differentiate the equation $\cos \theta =\dfrac{x}{5}$ with respect to $t$. The differentiation is as follows,
$\begin{aligned} & \dfrac{d(\cos \theta )}{dt}=\dfrac{d}{dt}\left( \dfrac{x}{5} \right) \\\ & -\sin \theta \dfrac{d\theta }{dt}=\dfrac{1}{5}\dfrac{dx}{dt} \\\ & \dfrac{d\theta }{dt}=\dfrac{1}{-\sin \theta }\cdot \dfrac{1}{5}\dfrac{dx}{dt} \\\ \end{aligned}$
Now, we know that $\dfrac{dx}{dt}=0.5$ m/sec. We also know that $\sin \theta =\dfrac{\text{Opposite}}{\text{Hypotenuse}}$ . The opposite side is the length of the wall upto the ladder's top, which is 4 m. Hence, $\sin \theta =\dfrac{4}{5}$. Substituting these values in the above equation, we get
$\begin{aligned} & \dfrac{d\theta }{dt}=\dfrac{5}{-4}\times \dfrac{1}{5}\times 0.5 \\\ & =\dfrac{-1}{4}\times \dfrac{1}{2} \\\ & =\dfrac{-1}{8} \end{aligned}$
Hence, the rate of change in the angle between the ladder and the ground is $\dfrac{d\theta }{dt}=\dfrac{-1}{8}$ m/sec.

So, the correct answer is “Option A”.

Note: The negative sign in the rate of change in the angle between the ladder and the ground indicates that the angle is decreasing, as we had expected. Coming up with the equation that relates the necessary variables is a difficult task. Drawing rough diagrams makes it useful in such questions.