Question
Question: If $x^3 - 6x^2 + 11x - 6$ is a prime number then the number of possible integral values of x is...
If x3−6x2+11x−6 is a prime number then the number of possible integral values of x is
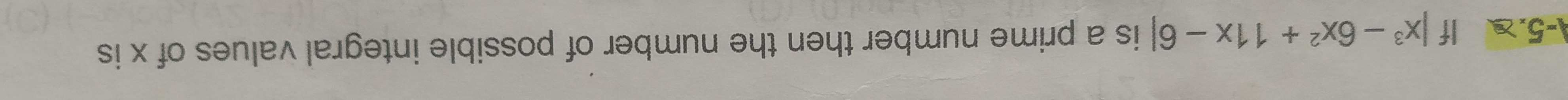
0
Solution
Let P(x)=x3−6x2+11x−6. We can factorize P(x) as follows:
P(x)=(x−1)(x−2)(x−3)
We are given that P(x) is a prime number. Let P(x)=p, where p is a prime number. p=(x−1)(x−2)(x−3). Since x is an integer, the factors (x−1),(x−2),(x−3) are integers.
We need to find the number of integral values of x for which P(x) is a prime number.
Consider the case where x=1,2,3. If x=1, P(1)=(1−1)(1−2)(1−3)=0. If x=2, P(2)=(2−1)(2−2)(2−3)=0. If x=3, P(3)=(3−1)(3−2)(3−3)=0. Since 0 is not a prime number, x=1,2,3 are not solutions.
If x>3, then x−1,x−2,x−3 are all positive integers greater than 0. Since x−1>x−2>x−3, we have x−3≥1, x−2≥2, x−1≥3. The product of three integers greater than 1 cannot be a prime number.
If x<1, then x−1,x−2,x−3 are all negative integers. Then (x−1)(x−2)(x−3) is a negative number, which cannot be a prime number.
Thus, there are no integral values of x for which P(x) is a prime number. Therefore, the number of possible integral values of x is 0.
Final Answer: The final answer is 0
