Question
Question: If $\Delta = \begin{vmatrix} a & b & c \\ c & a & b \\ b & c & a \end{vmatrix}$, then the value of $...
If Δ=acbbaccba, then the value of a2−bcc2−abb2−cab2−caa2−bcc2−abc2−abb2−caa2−bc is-
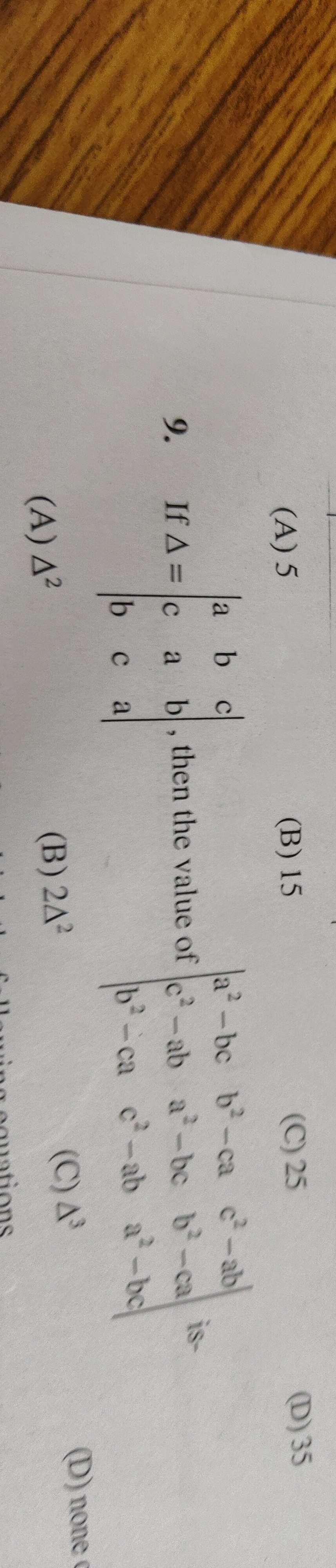
Δ2
2Δ2
Δ3
none of
Δ2
Solution
To solve this problem, we need to evaluate the given determinant in terms of Δ.
Let the first matrix be M: M=acbbaccba The determinant Δ=∣M∣=acbbaccba.
Now, let's look at the second determinant, let's call it D′: D′=a2−bcc2−abb2−cab2−caa2−bcc2−abc2−abb2−caa2−bc
We need to find the cofactors of the matrix M. The cofactor Aij of an element mij is given by (−1)i+j times the determinant of the submatrix obtained by removing the i-th row and j-th column.
Let's calculate the cofactors of M: A11=(−1)1+1acba=a2−bc A12=(−1)1+2cbba=−(ca−b2)=b2−ca A13=(−1)1+3cbac=c2−ab
A21=(−1)2+1bcca=−(ab−c2)=c2−ab A22=(−1)2+2abca=a2−bc A23=(−1)2+3abbc=−(ac−b2)=b2−ca
A31=(−1)3+1bacb=b2−ac=b2−ca A32=(−1)3+2accb=−(ab−c2)=c2−ab A33=(−1)3+3acba=a2−bc
Now, let's form the cofactor matrix C of M: C=A11A21A31A12A22A32A13A23A33=a2−bcc2−abb2−cab2−caa2−bcc2−abc2−abb2−caa2−bc
Notice that the determinant D′ is exactly the determinant of the cofactor matrix C, i.e., D′=∣C∣.
We know a property of determinants and adjoint matrices: For any square matrix M of order n, the determinant of its adjoint matrix, ∣adj(M)∣, is equal to ∣M∣n−1. Also, the adjoint matrix is the transpose of the cofactor matrix, i.e., adj(M)=CT. Therefore, ∣adj(M)∣=∣CT∣.
Since the determinant of a matrix is equal to the determinant of its transpose, ∣CT∣=∣C∣. So, we have D′=∣C∣=∣CT∣=∣adj(M)∣.
For the given matrix M, its order is n=3. Thus, ∣adj(M)∣=∣M∣3−1=∣M∣2. Since ∣M∣=Δ, we have ∣adj(M)∣=Δ2.
Combining these results, we get: D′=Δ2.
The final answer is Δ2.
