Question

A 4kg swing in a vertical circle at the end of the chord 1m long. Find out the maximum speed at which it can swing if the cord can sustain maximum tension of 140N.

Answer 1

when the swing of mass m undergoes in vertical circular motion, then tension equals the centripetal force and the weight acts in downward direction. At the bottom of the circle, tension is larger, and at upper positions it is small.

Formula used:
Tension in the string is given by:
$T=(M{{v}^{2}}/r)+Mg$

Complete answer:
A swing of mass moves in a vertical circle, the Tension in the string is equal to the centripetal force. Then the tension acts in downward direction and weight also acts in downward direction, also acceleration in centripetal force also acts in downward direction as shown in figure below:

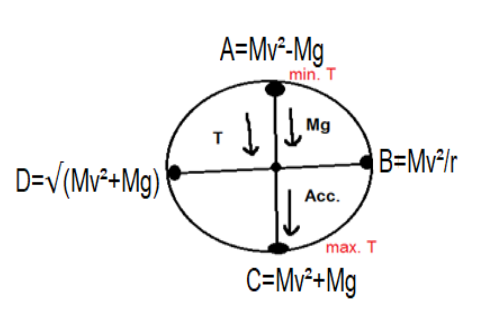
In the figure,
At point A, tension is given by:
$A=M{{v}^{2}}-Mg$
At point B, tension is given by:
$B=M{{v}^{2}}/r$
Also at point C, tension is given by:
$C=M{{v}^{2}}+Mg$
For point D, tension is given as:
$D=\sqrt{(M{{v}^{2}}+Mg)}$
Tension at top point A is small as compared to point C.

The weight of the swing acts in downward direction which can be resolved into two components, i.e. horizontal and vertical components. Horizontal component is balanced by the tension, and the remaining force provides the object to move in a vertical circle.

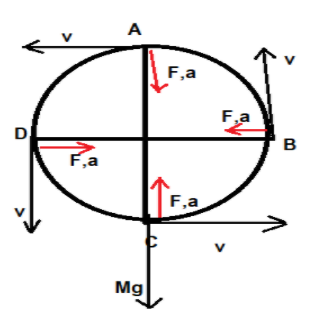
Now the force in Y- direction is given by:
$\begin{aligned} & \sum{{{F}_{y}}=T-Mg} \\\ & M{{A}_{c}}=T-Mg \\\ & M({{v}^{2}}/r)=T-Mg \\\ & T=(M{{v}^{2}}/r)+Mg \\\ \end{aligned}$
Therefore, at points A and B there is lesser speed and there is lesser amount of tension.
At the bottom (i.e. at point C), there is maximum tension and the velocity gets increased.
Now to find velocity, we use
$\begin{aligned} & T=(M{{v}^{2}}/r)+Mg \\\ & 140N=(4{{v}^{2}}/1m)+4\times 10 \\\ & {{v}^{2}}=(140-40)/4 \\\ & {{v}^{2}}=25 \\\ & v=5m{{s}^{-1}} \\\ \end{aligned}$
Therefore, maximum speed at which it can swing is $v=5m{{s}^{-1}}$

Note:
A swing moves in a vertical circle, the tension at various positions varies. The tension at the top position is lesser as compared to the bottom position where tension is greater. Tension depends on the centripetal force and weight of the swing.